Випадок скінченної кількості вимірювань
На практиці кількість вимірювань ніколи не буває нескінченно великою, а тому середнє арифметичне 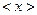 вже не буде дорівнювати справжньому значенню виміряної величини
вже не буде дорівнювати справжньому значенню виміряної величини 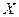 (найбільш імовірному значенню).
(найбільш імовірному значенню).
Наскільки близьким буде середнє арифметичне до справжнього значення виміряної величини, тобто яка похибка у визначенні середнього арифметичного? Встановити це дає змогу теорія ймовірності.
Припустимо, що проведено вимірювання фізичної величини 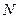 разів. Середнє значення у цій серії вимірювань дорівнюватиме
разів. Середнє значення у цій серії вимірювань дорівнюватиме 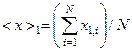 . Коли ми виконаємо таку серію вимірювань ще раз, то отримаємо інше середнє значення
. Коли ми виконаємо таку серію вимірювань ще раз, то отримаємо інше середнє значення 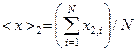 . Коли проведемо
. Коли проведемо 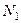 серій вимірювань, то отримаємо
серій вимірювань, то отримаємо 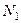 середніх значень:
середніх значень:
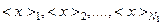 . (1.14)
. (1.14)
Виявляється, що такі середні значення, як і окремі результати вимірювань, описуються розподілом Гауса. При цьому найбільш імовірні значення цих розподілів збігаються, а дисперсії пов’язані співвідношеннями
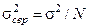 , (1.15)
, (1.15)
де 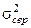 – дисперсія розподілу середніх арифметичних значень (1.14),
– дисперсія розподілу середніх арифметичних значень (1.14), 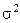 – дисперсія розподілу окремих значень.
– дисперсія розподілу окремих значень.
Таким чином, дисперсія середнього арифметичного залежить від кількості вимірювань 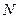 і зменшується зі збільшенням
і зменшується зі збільшенням 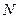 . Коли кількість вимірювань у серії
. Коли кількість вимірювань у серії 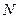 прямує до нескінченності, то, як випливає з (1.15),
прямує до нескінченності, то, як випливає з (1.15), 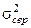 прямує до нуля. Це означає, у випадку
прямує до нуля. Це означає, у випадку 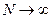 найбільш імовірне значення збігається із середнім арифметичним.
найбільш імовірне значення збігається із середнім арифметичним.
Для визначення дисперсії розподілу середніх арифметичних значень використовують середньоквадратичну похибку середнього арифметичного, яку визначають зі співвідношення
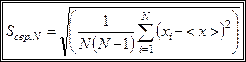 (1.15)
(1.15)
(порівняйте із середньоквадратичною похибкою окремого вимірювання (1.9)). Можна показати, що при достатньо великій кількості вимірювань 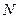 дисперсія розподілу середніх арифметичних значень і середньоквадратична похибка середнього арифметичного пов’язані між собою співвідношенням
дисперсія розподілу середніх арифметичних значень і середньоквадратична похибка середнього арифметичного пов’язані між собою співвідношенням
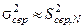 . (1.16)
. (1.16)
Зазначимо, для розподілу окремих вимірювань, як випливає з (1.11), спостерігається аналогічне співвідношення
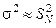 . (1.17)
. (1.17)
Кількість вимірювань під час виконання лабораторної роботи обмежена і рідко перевищує 10, а найчастіше виконують лише 5 вимірювань. Формули для дисперсії 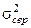 (1.16) та
(1.16) та 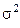 (1.17) є правильними лише коли
(1.17) є правильними лише коли 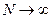 , тобто для великих чисел
, тобто для великих чисел 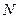 . Для малих чисел
. Для малих чисел 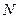 ці рівності порушуються. Тому для знаходження меж довірчого інтервалу для малих значень
ці рівності порушуються. Тому для знаходження меж довірчого інтервалу для малих значень 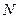 ми не можемо користуватися коефіцієнтом
ми не можемо користуватися коефіцієнтом 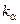 (1.13), тому що дисперсія в цьому разі є невідомою.
(1.13), тому що дисперсія в цьому разі є невідомою.
Тому для знаходження меж довірчого інтервалу потрібно використати подібне до (1.13) співвідношення
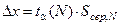 , (1.18)
, (1.18)
де 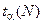 є коефіцієнтом, на який потрібно помножити середньоквадратичну похибку середнього арифметичного, щоб при обраній довірчій імовірності дістати значення напівширини довірчого інтервалу. Цей коефіцієнт отримав назву коефіцієнта Стьюдента на честь англійського математика Госсета, який розв’язав вище-сформульовану задачу і опублікував свою працю під псевдонімом Стьюдента.
є коефіцієнтом, на який потрібно помножити середньоквадратичну похибку середнього арифметичного, щоб при обраній довірчій імовірності дістати значення напівширини довірчого інтервалу. Цей коефіцієнт отримав назву коефіцієнта Стьюдента на честь англійського математика Госсета, який розв’язав вище-сформульовану задачу і опублікував свою працю під псевдонімом Стьюдента.
Коефіцієнт Стьюдента 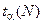 залежить як від кількості вимірювань
залежить як від кількості вимірювань 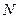 , так і від довірчої імовірності
, так і від довірчої імовірності 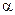 . У табл. 1.2 наведено значення коефіцієнтів Стьюдента для різної кількості вимірювань та для різних значень довірчої ймовірності.
. У табл. 1.2 наведено значення коефіцієнтів Стьюдента для різної кількості вимірювань та для різних значень довірчої ймовірності.
Користуватися табл. 1.2 потрібно так. Обчисливши середньоквадратичну похибку середнього значення ( 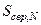 ), потрібно задатися довірчою ймовірністю
), потрібно задатися довірчою ймовірністю 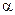 та за табл. 1.2 для відповідної кількості вимірювань
та за табл. 1.2 для відповідної кількості вимірювань 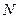 знайти коефіцієнт Стьюдента. Далі знаходимо випадкову похибку результату прямих вимірювань, яка дорівнює півширині довірчого інтервалу:
знайти коефіцієнт Стьюдента. Далі знаходимо випадкову похибку результату прямих вимірювань, яка дорівнює півширині довірчого інтервалу:
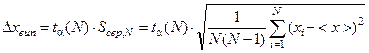 . (1.19)
. (1.19)
На практиці часто використовують значення коефіцієнта Стьюдента, що дорівнює трьом ( 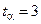 ). У цьому разі ймовірність потрапляння середнього значення у довірчий інтервал із напівшириною (1.20) змінюється від
). У цьому разі ймовірність потрапляння середнього значення у довірчий інтервал із напівшириною (1.20) змінюється від 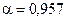 при
при 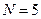 до
до 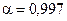 при
при 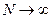 (табл. 1.1). Тому в разі, якщо кількість вимірювань не менша ніж п’ять, використовують для обчислення абсолютної похибки формулу
(табл. 1.1). Тому в разі, якщо кількість вимірювань не менша ніж п’ять, використовують для обчислення абсолютної похибки формулу
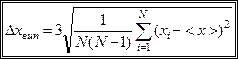 . (1.20)
. (1.20)
Таблиця 1.2
| Кількість дослідів N | Коефіцієнт Стьюдента tα(N) | |||||
| Ймовірність α | ||||||
| 0,5 | 0,7 | 0,8 | 0,90 | 0,95 | 0,99 | |
| 1,00 | 2,0 | 3,1 | 6,3 | 12,7 | 63,7 | |
| 0,82 | 1,3 | 1,9 | 2,9 | 4,3 | 9,9 | |
| 0,77 | 1,2 | 1,6 | 2,4 | 3,2 | 5,8 | |
| 0,74 | 1,2 | 1,5 | 2,1 | 2,8 | 4,6 | |
| 0,73 | 1,1 | 1,4 | 2,0 | 2,6 | 4,0 | |
| 0,72 | 1,1 | 1,4 | 1,9 | 2,4 | 3,7 | |
| 0,71 | 1,1 | 1,4 | 1,9 | 2,4 | 3,5 | |
| 0,71 | 1,1 | 1,4 | 1,9 | 2,3 | 3,4 | |
| 0,70 | 1,1 | 1,4 | 1,8 | 2,3 | 3,3 | |
| 0,68 | 1,1 | 1,3 | 1,7 | 2,0 | 2,7 | |
| 0,68 | 1,0 | 1,3 | 1,7 | 2,0 | 2,6 | |
| ∞ | 0,67 | 1,0 | 1,3 | 1,6 | 2,0 | 2,6 |
Алгоритм розрахунку випадкової похибки за допомогою формули (1.20) також називають правилом “трьох сигм”. Його будемо використовувати для знаходження випадкової похибки вимірювання.
Результати вимірювань подаємо у вигляді
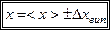 . (1.21)
. (1.21)
Співвідношення означає, що середнє арифметичне значення фізичної величини потрапляє в інтервал 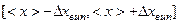 з імовірністю більшою за 0,95 (
з імовірністю більшою за 0,95 ( 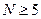 ).
).
Дата добавления: 2015-05-05; просмотров: 1017;
