Оцінювання похибок непрямих вимірювань
У більшості випадків величину, що нас цікавить, безпосередньо виміряти не можна. Вимірюються інші величини, які пов'язані певним співвідношенням із шуканою величиною, при цьому похибки безпосередньо вимірюваних величин відомі. Шукану величину знаходимо шляхом розрахунків за допомогою відомого співвідношення. Такі вимірювання, як було зазначено вище, називають непрямими вимірюваннями.
Загальні правила обчислення похибок непрямих вимірювань можна отримати за допомогою математичної теорії похибок і методів диференціального числення. У цьому розділі ми не будемо розглядати теоретичне обґрунтування тих або інших формул, а просто наведемо ці формули в готовому вигляді та покажемо, як ними користуватися.
Нехай шукана величина 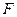 залежить від величин
залежить від величин 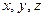 і обчислюється за відомою формулою
і обчислюється за відомою формулою
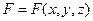 , (1.24)
, (1.24)
де 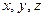 визначені за допомогою прямих вимірювань:
визначені за допомогою прямих вимірювань:
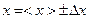 ,
, 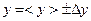 ,
, 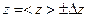 . (1.25)
. (1.25)
З’ясуємо, як визначити справжнє (найбільш імовірне) значення величини та її похибку 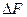 ?
?
Справжнє (найбільш імовірне) значення <F>, як це випливає з теорії ймовірностей, знаходять як відповідну функцію від середніх величин:
 , (1.26)
, (1.26)
а абсолютну похибку – з формули
 , (1.27)
, (1.27)
де 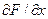 ,
,  ,
, 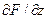 – частинні похідні функції. Нагадаємо, що при обчисленні частинної похідної, наприклад
– частинні похідні функції. Нагадаємо, що при обчисленні частинної похідної, наприклад 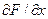 , усі інші змінні, крім x, вважаються незалежними.
, усі інші змінні, крім x, вважаються незалежними.
Формули (1.26) та (1.27) неважко узагальнити на випадок чотирьох та більше змінних.
Остаточний результат вимірювань записується у вигляді
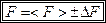 .
.
Дата добавления: 2015-05-05; просмотров: 949;
