Приклад: похибка вимірювання густини циліндра

Застосуємо співвідношення (1.26), (1.27) для знаходження середнього значення густини циліндра та її похибки. Густина циліндра обчислюється за формулою

.

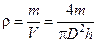У цій формулі вважаємо відомими з прямих вимірювань масу циліндра 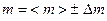, його діаметр 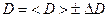та висоту .

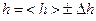Тоді, виходячи з формули (1.26), отримаємо

.

Застосуємо співвідношення (1.27) для визначення :

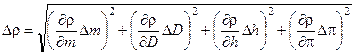. (1.28)

Далі знайдемо частинні похідні, що входять до (1.28):

; ;

; .

Підставляємо отримані вирази до (1.28):

.

Таким чином,

. (1.29)

Тут ураховано, що під час розрахунків ми використовуємо не точне значення числа , а його наближене (наприклад, ). Тоді абсолютна похибка числа буде дорівнювати

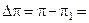3,14159265358979323846264338…–
– 3,1415 = 0,00009265358979323846264338… 0,000093.

Коли в лабораторній роботі для розрахунків використовуємо число з урахуванням восьми й більше знаків після коми, то похибка цього числа стає набагато меншою від похибки інших величин і в багатьох випадках її можна не враховувати.