Прийнято, що число середнього значення величини округлюють так, щоб останніми праворуч залишалися цифри тих розрядів, які збереглися в похибці після її округлення.

Виходячи з того, що після округлення похибка має значення 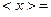0,0007, то середнє значення округлюємо до 4-ї цифри після коми включно, тобто 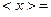2,8675. Таким чином, величина 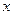повинна бути записана як

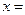2,8675 ± 0,0007. (1.32)

Іноді вираз (1.32) записують в еквівалентній формі

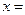2,8675(7), (1.33)

де в дужках зазначена похибка останнього знака.

Вирішимо питання: скільки значущих цифр потрібно використовувати під час розрахунків?

Зрозуміло, що результат вимірювань потрібно округлювати. Проте будь-яке округлення додає систематичну похибку. Якщо ми будемо округлювати результати проміжних обчислень, то ця систематична похибка накопичуватиметься. Тому потрібно використати правило: всі проміжні обчислення повинні мати на одну значущу цифру більше, ніж результати, отримані під час вимірювань. Це правило стосується як оброблення результатів прямих вимірювань, так і особливо непрямих вимірювань, оскільки тут кількість проміжних обчислень буває набагато більшою.