При побудові графіка необхідно дотримуватися таких правил.

1 Графік необхідно будувати лише на папері, що має координатну сітку, наприклад на міліметровому папері. Графіки будують олівцем. Також для побудови графіків можна використовувати відповідні комп’ютерні програми.

2 Уздовж горизонтальної осі графіка відкладаються значення незалежної змінної, вздовж вертикальної – значення функції цієї змінної. Для вибору масштабу уздовж кожної осі спочатку необхідно визначити діапазон зміни значень вимірюваних величин. При цьому діапазон зміни значень потрібно вибрати так, щоб значення експериментальних точок максимально заповнювали вибрані інтервали кожної осі. На кожній осі графіка через однакові інтервали наносяться масштабні мітки. Біля координатних осей вказують символи (позначення) величин і, через кому, одиниці їх вимірювань.

3 Після того як проставлені масштабні мітки й зазначені позначення осей з одиницями вимірювань, на графік наносяться експериментальні точки. При цьому числові значення величин, що відповідають експериментальним точкам, на осях не проставляються. Бажано, щоб інтервали між експериментальними точками, які відкладаються вздовж осі абсцис, були приблизно однаковими.

4 Крім самих експериментальних точок, на графіках біля кожної точки зазначається довірчий інтервал, який відповідає цьому вимірюванню. Це виконується за допомогою горизонтальних і вертикальних рисок, що перетинаються в експериментальних точках (рис. 1.5). Довжина кожної риски дорівнює подвоєній похибці вимірювання відповідної величини. Якщо експериментальна точка отримана однократним вимірюванням, то похибка відповідної величини визначається похибкою приладу. Якщо ж експериментальна точка отримана в результаті багаторазових вимірів, то похибка відповідної величини визначається шляхом статистичного оброблення.

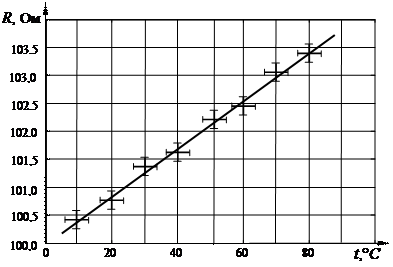
Рисунок 1.5

5 Якщо довірчі інтервали є дуже малими в обраному масштабі осей координат, експериментальні точки на графіку проставляються у вигляді маленьких кружечків (трикутників і т. д.) із центром у точках, що відповідають експериментальним даним.

6 Через нанесений на графік масив експериментальних точок проводять плавну, без зламів, криву так, щоб вона проходила через довірчі інтервали всіх або більшості експериментальних точок. Існують точні математичні методи, що дозволяють побудувати за отриманими експериментальними точками “найкращу” криву. Однак і, не використовуючи такі методи, можна наближено побудувати криву, досить близьку до “найкращої”. Справа в тому, що в лабораторному практикумі очікувана залежність найчастіше відома, тому зрозуміло, яку криву потрібно будувати. Основне правило полягає в тому, що криву потрібно будувати так, щоб кількість точок, що лежать вище та нижче кривої, була приблизно однаковою. На рис. 1.5 показано приклад графіка експериментальної залежності опору металу від температури.

7 За допомогою графіків можна проводити оброблення експериментальних результатів. Для цього вздовж осей відкладають величини так, щоб експериментальна крива була близькою до прямої. Потім будують пряму, яка проходить через довірчі інтервали всіх або більшості експериментальних точок. Кількість точок, що лежать вище й нижче прямої, повинна бути приблизно однаковою. Далі вимірюють тангенс нахилу отриманої експериментально прямої і знаходять характеристику досліджуваного процесу. Так, на рис. 1.5 тангенс нахилу залежності опору від температури визначає температурний коефіцієнт опору металу.

Контрольні питання[1]⁾

1 Що розуміють під вимірюванням фізичної величини?

2 Пояснити терміни: абсолютна похибка вимірювання, відносна похибка вимірювання.

3 Які вимірювання називають прямими, які – непрямими?

4 Які похибки відносять до систематичних?

5 Які похибки відносять до випадкових?

6 Які похибки відносять до грубих?

7 Пояснити терміни: ймовірність, функція розподілу ймовірностей, найбільш імовірна величина.

8 Записати функцію розподілу Гауса. Поясніть позначення. Як пов’язаний розподіл Гауса з вимірюванням фізичних величин?

9 Записати формули для середнього арифметичного значення, середньоквадратичної похибки окремого вимірювання? Поясніть позначення. З якими ймовірнісними характеристиками вимірювання пов’язані ці величини?

10 Пояснити терміни: довірчий інтервал, довірча ймовірність?

11 Що розуміють під похибкою середнього арифметичного значення, дисперсією середнього арифметичного значення? Як визначити середньоквадратичну похибку середнього арифметичного?

12 Призначення коефіцієнта Стьюдента. Від яких параметрів він залежить?

13 Пояснити правило “трьох сигм”. У якому вигляді потрібно подавати результати вимірювань?

14 Як знаходять похибку вимірювань у разі наявності як випадкових, так і систематичних похибок?

15 Як знаходити абсолютну похибку непрямих вимірювань? Записати відповідну формулу. Поясніть позначення.

16 Густину циліндра можна визначити за формулою 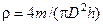, визначивши його масу 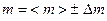, діаметр 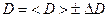та висоту 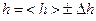за допомогою прямих вимірювань. Знайти абсолютну похибку вимірювання густини циліндра.

17 Густину кулі можна визначити за формулою 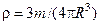, визначивши її масу 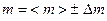та радіус 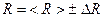за допомогою прямих вимірювань. Знайти абсолютну похибку вимірювання густини кулі.

18 Густину конуса можна визначити за формулою 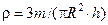, визначивши його масу 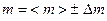, радіус основи 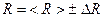та висоту 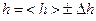за допомогою прямих вимірювань. Знайти абсолютну похибку вимірювання густини конуса.

19 Якою величиною характеризується точність приладів? Дайте цій величині визначення, пояснення.

20 Які цифри називають значущими? Наведіть приклад. Скільки цифр потрібно залишати у записі абсолютної похибки?

21 Поясніть правила округлення.

22 Поясніть, скільки цифр потрібно залишати у записі середнього значення фізичної величини? Скільки цифр потрібно враховувати у проміжних обчисленнях?

23 Яких правил потрібно дотримуватися при побудові графіка? Як за допомогою графіків проводять оброблення експериментальних результатів?

24 Величина y визначається за формулою y = a×(b+c)². Знайти середнє значення величини y та її абсолютну похибку, якщо b = 7,00 ± 0,04; c = 13,00 ± 0,03, а при п'ятикратному вимірюванні значення a отримано: a₁ = 1,02; a₂ = 1,00; a₃ = 0,97; a₄ = 0,98; a₅ = 1,03.

25 Величина y визначається за формулою y = (a+b)/(d–c). Знайти середнє значення величини y та її абсолютну похибку, якщо b = 7,0 ± 0,4; c = 3,0 ± 0,5; d = 6,0 ± 0,6, а при п'ятикратному вимірюванні значення a отримано: a₁ = 2,3; a₂ = 1,8; a₃ = 1,7; a₄ = 2,0; a₅ = 2,2.

26 Величина y визначається за формулою y = a² (b+c) / d. Знайти середнє значення величини y та її абсолютну похибку, якщо b = 3,0±0,5; c = 4,0±0,2; d = 7,0±0,7, а при п'ятикратному вимірюванні значення a отримано: a₁ = 10,2; a₂ = 9,8; a₃ = 9,7; a₄ = 10,0; a₅ = 10,3.