Amp; 6.5. Означення визначеного інтеграла як границі інтегральної суми.
Нехай функція 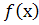 визначена на відрізку
визначена на відрізку 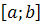 . Розіб’ємо відрізок
. Розіб’ємо відрізок 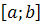 на n частин точками
на n частин точками 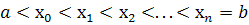 , виберемо на кожному елементарному відрізку
, виберемо на кожному елементарному відрізку 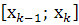 довільну точку
довільну точку 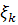 і позначимо через
і позначимо через 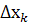 довжину кожного такого відрізка. Інтегральною сумою для функції
довжину кожного такого відрізка. Інтегральною сумою для функції 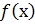 на відрізку
на відрізку 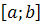 називається сума вигляду
називається сума вигляду
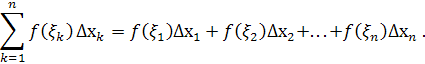
Визначеним інтегралом від функції 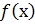 на відрізку
на відрізку 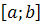 називається границя інтегральної суми при умові, що довжина найбільшого з елементарних відрізків прямує до нуля :
називається границя інтегральної суми при умові, що довжина найбільшого з елементарних відрізків прямує до нуля :
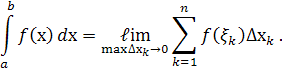
Для будь-якої функції 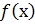 , неперервної на відрізку
, неперервної на відрізку 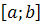 , завжди існує визначений інтеграл
, завжди існує визначений інтеграл 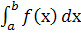 .
.
Наведемо основні властивості визначеного інтеграла.
10. Визначений інтеграл від алгебраїчної суми скінченного числа функцій дорівнює алгебраїчній сумі визначених інтегралів від функцій, що додаються :
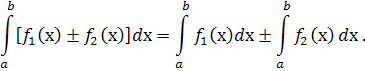
20. Сталий множник можна винести за знак визначеного інтеграла :
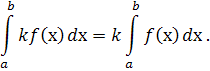
30. При перестановці меж інтегрування визначений інтеграл змінює знак на протилежний :
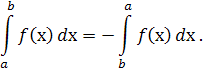
40. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю :
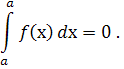
50. Відрізок інтегрування можна розбивати на частини :
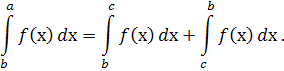
Для обчислення визначеного інтеграла від функції 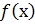 в тому випадку, коли можна знайти відповідний невизначений інтеграл
в тому випадку, коли можна знайти відповідний невизначений інтеграл 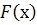 , є формула Ньютона – Лейбніца :
, є формула Ньютона – Лейбніца :
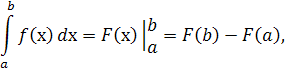
тобто визначений інтеграл дорівнює різниці значень первісної при верхній і нижній межах інтегрування.
Приклад 1. Обчисліть інтеграл :
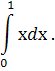
Розв’язання.
За формулою Ньютона – Лейбніца дістанемо :
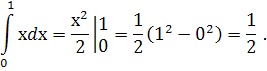
Дата добавления: 2015-06-27; просмотров: 3096;
