Властивості невизначеного інтеграла.
1. Невизначений інтеграл від диференціала функції дорівнює цій функції плюс довільна стала :
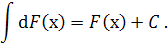
1. Диференціал невизначеного інтеграла дорівнює підінтегральному виразу :
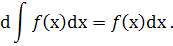
2. Невизначений інтеграл алгебраїчної суми функцій дорівнює алгебраїчній сумі невизначених інтегралів цих функцій :
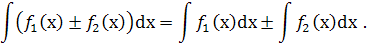
3. Сталий множник можна виносити за знак невизначеного інтеграла :
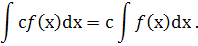
Amp; 6.2. Таблиця невизначених інтегралів.
1.  7.
7. 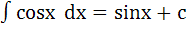
2. 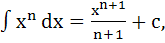 n
n 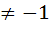 8.
8. 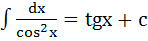
3. 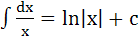 9.
9. 
4. 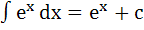 10.
10. 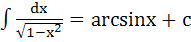
5. 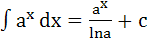 11.
11. 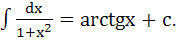
6. 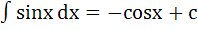
Приклад 1. Знайти інтеграл 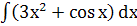 .
.
Розв’язання.
Застосовуючи третю і четверту властивість і формули (1) і (7), маємо
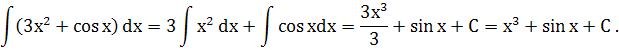
Дата добавления: 2015-06-27; просмотров: 1342;
