Розв’язування прикладних задач на мінімум і максимум.
Задача 1. Розбити число 24 на два доданки, добуток яких є найбільшим.
Розв’язання.
Позначимо один доданок через х , тоді другий буде 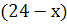 . Добуток цих доданків позначимо у:
. Добуток цих доданків позначимо у:
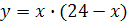 .
.
Потрібно знайти таке х, щоб функція у була найбільшою, тобто знайти максимум функції.
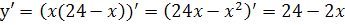 .
.
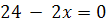 , звідси
, звідси 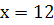 .
.
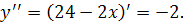
Отже функція при 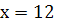 має максимум. Число 24 потрібно розбити на два рівних доданки, тоді добуток їх буде найбільшим.
має максимум. Число 24 потрібно розбити на два рівних доданки, тоді добуток їх буде найбільшим.
Задача 2. Із квадратного листа заліза, сторона якого дорівнює 30 см, треба вирізати в кожному куті такі квадрати, щоб після згинання країв отримати ящик найбільшої місткості.
| 30 см |
| х |

| х |
| 30 – 2х |
Позначимо через х довжину сторони того квадрата, який слід відрізати, а через 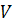 об’єм ящика. Тоді
об’єм ящика. Тоді 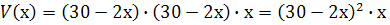 .
.
Потрібно знайти таке х, щоб функція 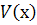 набувала найбільшого значення. Обчислимо похідну функції :
набувала найбільшого значення. Обчислимо похідну функції :
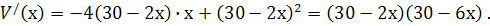
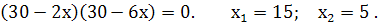
Точка 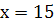 не задовольняє умову задачі.
не задовольняє умову задачі.
При 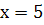 функція
функція 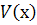 має максимум, так як похідна при переході аргумента через цю точку змінює знак з плюса на мінус.
має максимум, так як похідна при переході аргумента через цю точку змінює знак з плюса на мінус.
При 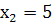 функція
функція 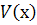 набуває найбільшого значення, яке дорівнює
набуває найбільшого значення, яке дорівнює 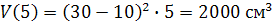 .
.
Питання для самоконтролю
1. Дати означення границі функції.
2. Сформулювати основні теореми про границі.
3. Дати означення функції, неперервної в точці.
4. Класифікація точок розриву.
5. Дати означення похідної.
6. Який фізичний зміст похідної?
7. Який геометричний зміст похідної?
8. Записати основні правила диференціювання функцій.
9. Записати формули похідних основних елементарних функцій.
10. Дати означення диференціалу функції.
11. Який геометричний зміст диференціалу функції?
12. Дати означення другої похідної.
13. Який механічний зміст другої похідної?
14. Сформулювати умови зростання і спадання функції.
15. Сформулювати правило дослідження функції на екстремум.
16. Яка функція називається опуклою вниз (вгору)?
17. Сформулювати правило знаходження точок перегину графіка функції.
18. Як знайти найбільше і найменше значення функції на відрізку?
Дата добавления: 2015-06-27; просмотров: 3207;
