I. Решение логических задач средствами алгебры логики

Обычно используется следующая схема решения:

1. изучается условие задачи;

2. вводится система обозначений для логических высказываний;

3. конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;

4. определяются значения истинности этой логической формулы;

5. из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.

Пример 1. Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок.

— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.

— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.

Питер, к которому обратился Ник, возмутился:

— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.

По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?

Решение. Введем обозначения для логических высказываний:

Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.

Реплика Ника "Алези пилотирует самую мощную машину" не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.

Зафиксируем высказывания каждого из друзей:

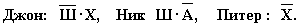
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание

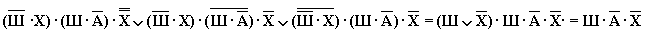
Высказывание 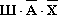истинно только при Ш=1, А=0, Х=0.

Ответ. Победителем этапа гонок стал Шумахер.