Amp; 4.2. Задачі лінійного програмування.
Задача.Для забезпечення трьох районів міста хлібом є два хлібзаводи. Першому району кожного дня потрібно 26 т хліба,другому – 14 т, третьому – 10 т. Хлібзавод №1 випікає щодня 30 т хліба, а хлібзавод №2 – 20 т. Вартість в гривнях доставки однієї тони хліба з кожного хлібзавода кожному району приведена в таблиці:
Таблиця 1
| Район Хлібзавод | |||
| №1 | |||
| №2 | 5 |
Потрібно скласти найбільш економний план перевозки хліба.
Розв’язання.
Позначимо через х число тон хліба, яке буде перевозитися з хлібзаводу №1 в перший район, а через у – число тон хліба, яке буде перевозитися з цього хлібзавода в другий район. Тоді в третій район із хлібзавода №1 буде перевозитися 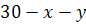 тон. Так як перший район кожного дня споживає 26 тон хліба, то 26-х тон потрібно перевезти із хлібзавода №2. Аналогічно, із хлібзавода №2 у другий район потрібно перевезти 14 – у тон хліба, а в третій район
тон. Так як перший район кожного дня споживає 26 тон хліба, то 26-х тон потрібно перевезти із хлібзавода №2. Аналогічно, із хлібзавода №2 у другий район потрібно перевезти 14 – у тон хліба, а в третій район 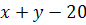 тон хліба.
тон хліба.
План перевозки хліба можна представити таблицею 2.
Таблиця 2
| Район Хлібзавод | |||
| №1 | x | y | 30-x-y |
| №2 | 26-x | 14-y | x+y-20 |
Вартість всієї перевозки S дорівнює сумі попарних добутків чисел із таблиці 1 на відповідні числа таблиці 2.
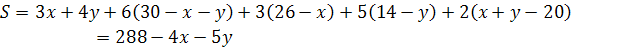
Так як кількість хліба, що завозиться в район не може бути від’ємною , то всі числа таблиці 2 повинні бути невід’ємні.
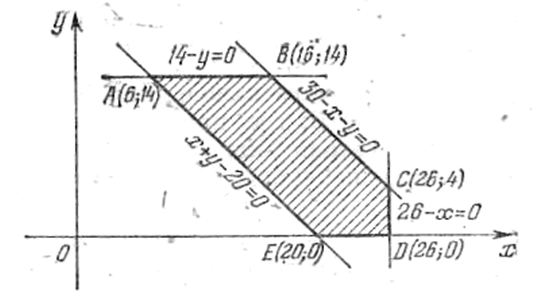
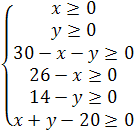
Розв’язком системи є точки многокутника АВСДЕ.
Функція S приймає найменше значення в одній із вершин многокутника АВСДЕ.
Знайдемо значення S в кожній із вершин.
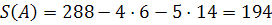
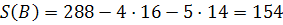
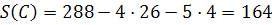
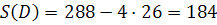
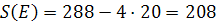
Найменше значення S=154 в точці В(16;14), тобто x=16; y=14
Найбільш економний план перевозки хліба можна подати таблицею 3.
Таблиця №3
| Район Хлібзавод | |||
| №1 | 16 | 14 | 0 |
| №2 | 10 | 0 | 10 |
Дата добавления: 2015-06-27; просмотров: 2124;
