Amp; 3.11. Гіпербола
Означення. Гіперболою називають множину точок площини, абсолютна величина різниці відстаней яких до двох даних точок, що називаються фокусами, є величина стала (2 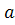 ), менша за відстань між фокусами (2с).
), менша за відстань між фокусами (2с).
|
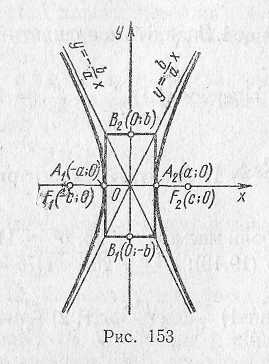
Рівняння гіперболи, фокуси якої лежать на осі ОХ, має вигляд
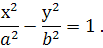
де 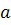 - довжина дійсної півосі;
- довжина дійсної півосі; 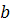 - довжина уявної півосі.
- довжина уявної півосі.
Залежність між параметрами 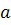 ,
, 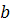 і с визначається співвідношенням
і с визначається співвідношенням
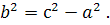
Ексцентриситетом гіперболи називається відношення фокусної відстані до її дійсної осі :
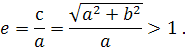
Гіпербола має дві асимптоти, рівняння яких
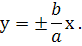
Якщо дійсна і уявна осі гіперболи рівні (тобто 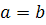 ), то гіпербола називається рівносторонньою і її рівняння записують у вигляді
), то гіпербола називається рівносторонньою і її рівняння записують у вигляді
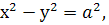
а рівняння її асимптот
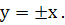
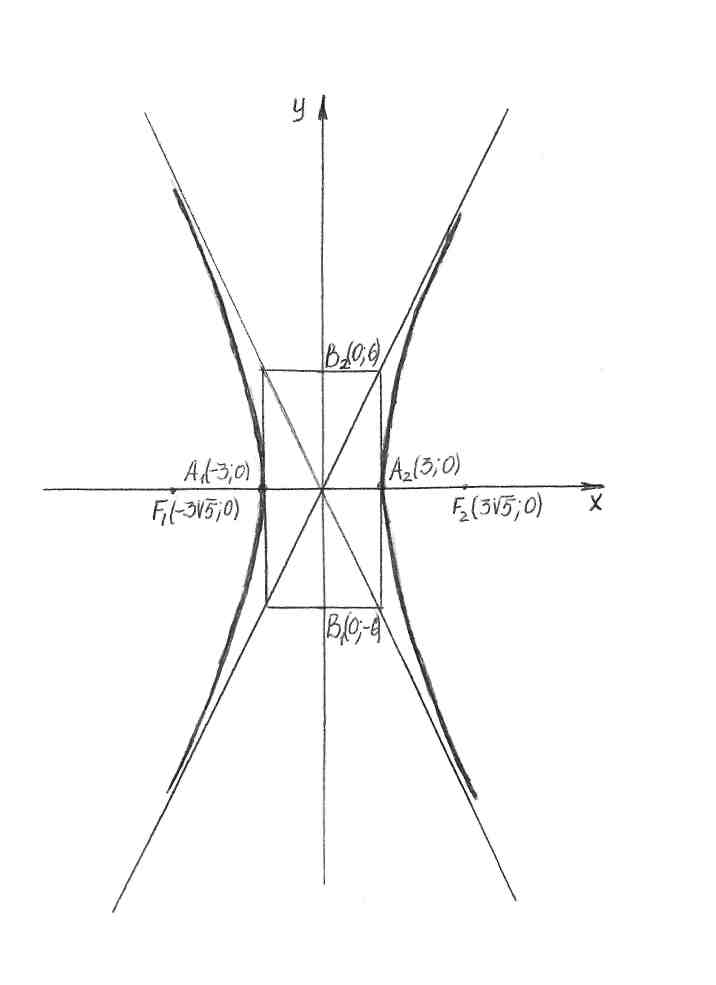
Приклад 13. Складіть рівняння гіперболи, якщо її вершини лежать у точках (-3; 0) і (3; 0), а фокуси – в точках 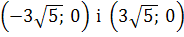 . Побудуйте малюнок.
. Побудуйте малюнок.
Розв’язання.
Із умови випливає, що 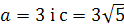 . За формулою
. За формулою 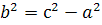 маємо
маємо 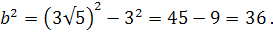
 Підставимо ці значення в рівняння гіперболи, дістанемо
Підставимо ці значення в рівняння гіперболи, дістанемо 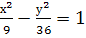 .
.
Дата добавления: 2015-06-27; просмотров: 2108;
