Amp; 3.12. Парабола

Означення. Параболою називають множину точок на площині, рівновіддалених від даної точки, яку називають фокусом, і від даної прямої, яку називають директрисою.

Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь ОХ і вітки напрямлені вправо має вигляд

,

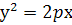де 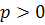(параметр параболи) – відстань від фокуса до директриси.

Рівняння її директриси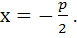

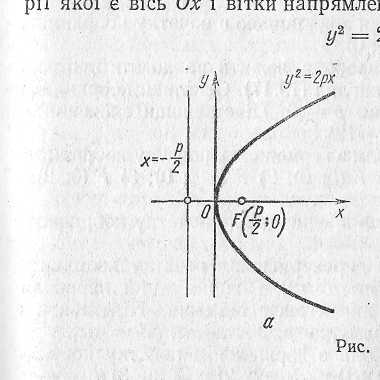
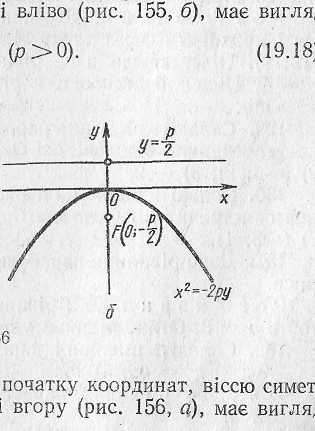
Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь ОХ і вітки напрямлені вліво, має вигляд

s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>p&gt;0</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t> .</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">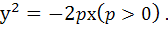

Рівняння її директриси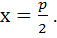

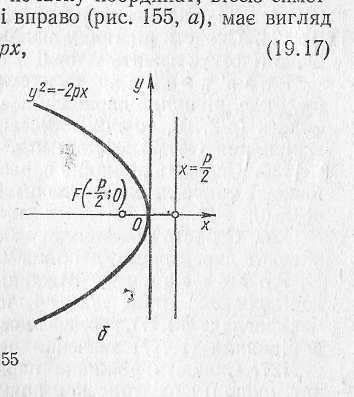
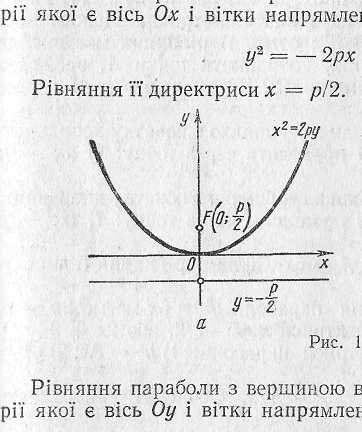
Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь ОУ і вітки напрямлені вгору, має вигляд

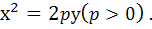
Рівняння її директриси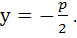

Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь ОУ і вітки напрямлені вниз, має вигляд

s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>p&gt;0</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t> .</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">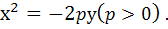

Рівняння її директриси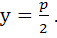

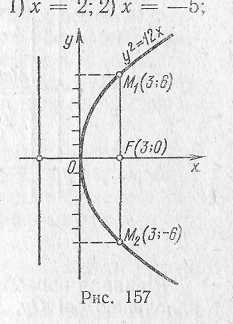
Приклад 14. Складіть рівняння параболи з вершиною в початку координат, якщо її фокус лежить в точці F(3;0). Побудуйте малюнок.

Розв’язання.

Рівняння параболи має вигляд 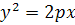. Оскільки координати фокуса 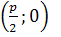, то 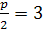, звідки 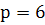. Підставимо значення р в рівняння, дістанемо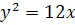

Питання для самоконтролю

1. Який вигляд має загальне рівняння прямої ?

2. Який вигляд має рівняння прямої з кутовим коефіцієнтом ?

3. Запишіть рівняння прямої, яка проходить через дві точки.

4. Запишіть канонічне рівняння прямої.

5. Який вигляд має рівняння прямої, яка проходить через дану точку з заданим нормальним вектором ?

6. Запишіть рівняння прямої у відрізках на осях.

7. За якою формулою обчислюється кут між двома прямими ?

8. Яка умова паралельності двох прямих ?

9. Яка умова перпендикулярності двох прямих ?

10. За якою формулою знаходиться відстань від точки до прямої ?

11. Які види рівнянь прямої в просторі ?

12. За якою формулою обчислюється кут між двома прямими в просторі ?

13. Яка умова паралельності двох прямих у просторі ?

14. Яка умова перпендикулярності двох прямих у просторі ?

15. Записати рівняння кола.

16. Записати рівняння еліпса.

17. Що називається ексцентриситетом еліпса ?

18. Записати рівняння гіперболи і її асимптот.

19. Що називається ексцентриситетом гіперболи ?

20. Записати рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь ОХ і вітки напрямлені вправо (вліво).

21. Записати рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь ОУ і вітки напрямлені вгору (вниз).