Никаких других формул в алгебре логики нет.
В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.
В качестве примера рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде (A v B) 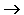 C. Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".
C. Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".
Как показывает анализ формулы (A v B) 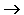 C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.
C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.
Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v 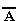 , соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
, соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
В качестве другого примера рассмотрим формулу А . 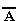 , которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо
, которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо 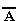 обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом "=" или символом " 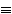 " Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
1. одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
2. на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации.
Мы уже рассмотрели способы записи двоичной информации на магнитных дисках и на CD-ROM.
В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:
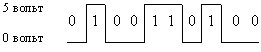
Дата добавления: 2015-05-08; просмотров: 1579;
