Асимптотические формулы.
При большом количестве испытаний n формула Бернулли не удобна для вычислений, поэтому применяется приближенные формулы, результаты которых тем точнее, чем больше n.
Формула Пуассона (для редких событий).
Пусть событие А может произойти в любом из n повторных независимых испытаний с постоянной вероятностью р, отличной от 0 и 1. Пусть количество испытаний n достаточно велико, а вероятность р мала, т.е. выполняются условия Пуассона:
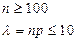 тогда справедлива формула Пуассона:
тогда справедлива формула Пуассона:
(15) 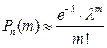
Замечания:
1. Функция, стоящая в правой части формулы 2 называется функцией Пуассона. Значение этой функции определяется по двум параметрам λ и m.
2. Формула 2 является приближенной, а формула 1 точной.
Пример:
Вероятность изготовления стандартной детали равна 0,995. Найти вероятность того, что среди 1000 деталей будет более 3-х браков.
Решение:
n = 1000 ≥ 100 ; m > 3; p = 0,005; q = 0,995;
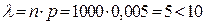
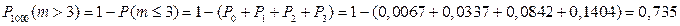
Дата добавления: 2015-05-26; просмотров: 1384;
