Интегральная теорема Муавра-Лапласа.
Пусть событие А может произойти в любом из M повторных независимых испытаниях с постоянной вероятностью р отличной от 0 и 1. Пусть количество испытаний велико, а события не редкие, т.е выполняются условия Муавра-Лапласа. Тогда вероятность того, что количество успехов заключено в некотором интервале определяется интегральной функцией Муавра-Лапласа.
(16) 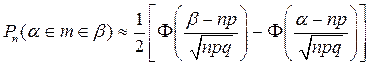
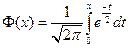 -интегральная функция Муавра-Лапласа Ошибка
-интегральная функция Муавра-Лапласа Ошибка
Свойства интегральной функции Муавра-Лапласа:
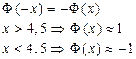
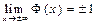
Пример:
Вероятность того, что деталь не пройдет контроль равна 0,2. Найти вероятность того, что среди 400 деталей число не прошедших контроль заключено в пределах от 70 до 100.
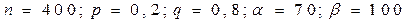
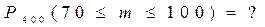
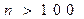
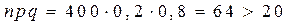
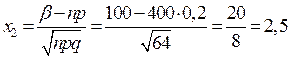
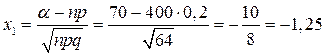
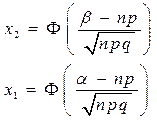 ?
?
Применим формулу 3 и подставим полученные данные.
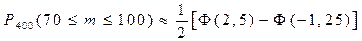
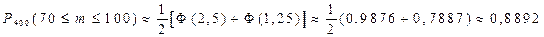
Следствие из интегральной теоремы Муавра-Лапласа:
1. Для симметричного интервала для числа успехов: 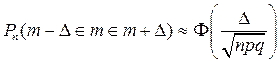
Пример:
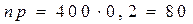 В условиях предыдущей задачи определить вероятность того, что число деталей не прошедших контроль заключено в пределах от 70 до 90.
В условиях предыдущей задачи определить вероятность того, что число деталей не прошедших контроль заключено в пределах от 70 до 90.
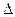 |  |
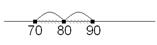 Применяя формулу 4 получаем:
Применяя формулу 4 получаем:
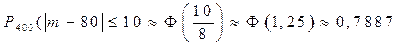
2. Для доли или частости успехов.
Если доля или частость успехов заключена в интервале, симметричном относительно р, то справедлива формула:

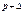
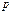
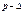
Задача № 1.
Вероятность того, что стрелок попадет в цель равна 0,7. Произведено 400 выстрелов. Найти вероятность того, что доля попаданий отклоняется от вероятности равной 0,7 не более чем на 0,04.
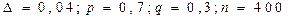

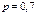
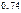
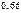
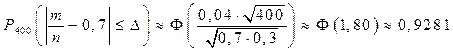
Ответ: С вероятностью 0,9281 можно утверждать, что доля попаданий отклоняется от вероятности равной 0,7 не более чем на 0,04.
Задача № 2.
В условиях предыдущей задачи определить, какой интервал для частости попаданий можно гарантировать с вероятностью 0,9281.
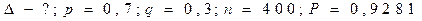

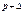
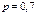
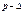
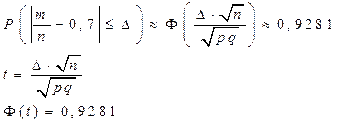
По таблице наоборот.
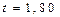
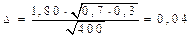
(19) 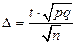 ;
;
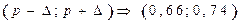
Ответ: Можно гарантировать интервал (0,66; 0,74) для доли попаданий с вероятностью 0,9281.
Задача № 3.
В условиях предыдущей задачи определить, сколько нужно произвести выстрелов, чтобы для доли попаданий гарантировать интервал (0,66; 0,74) с вероятностью 0,9281.
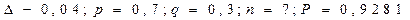
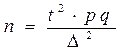
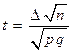
→ (7)
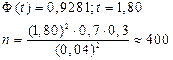
Ответ: Необходимо произвести 400 выстрелов, чтобы для доли попаданий гарантировать интервал (0,66; 0,74) с вероятностью 0,9281.
Дата добавления: 2015-05-26; просмотров: 1515;
