Операции над случайными величинами.
Пусть даны две случайные независимые величины Х и Y. Две случайные величины являются независимыми, если независимыми являются события, составляющие любой порядок их событий.
1. умножение на число – значения случайных величин умножаются на это число, а их вероятности не изменяются;
2. возведение в натуральную степень (квадрат, куб и т.д) – значения возводятся в степень, а вероятности не изменяются;
3. сложение, вычитание, умножение независимых случайных величин – значения попарно складываются, а соответствующие вероятности перемножаются;
Пример:
Даны две независимые случайные величины Х и Y. Составить закон распределения случайной величины Z = 2X + Y.
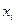
| -1 | ||
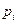
| 0,3 | 0,2 | 0,5 |
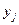
| ||
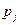
| 0,2 | 0,8 |
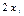
| -2 | ||||
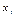
| -1 | ||||
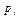
| 0,3 | 0,2 | 0,5 | ||
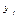
| 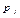
| ||||
| 0,2 | 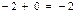
| 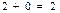
| |||
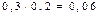
| 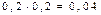
| 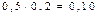
| |||
| 0,8 | 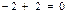
| 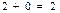
| 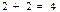
| ||
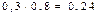
| 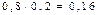
| 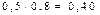
| |||
| Z | -2 | |||
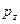
| 0,06 | 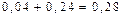
| 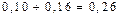
| 0,4 |
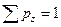
Дата добавления: 2015-05-26; просмотров: 1583;
