Числовые характеристики суммы и среднего арифметического случайных величин.

Пусть заданы n независимых случайных величин X₁, Х₂, …, Х_n имеющих математические ожидания a₁, a₂, …, a_n и дисперсии σ², σ²,…, σ². рассмотрим

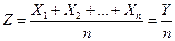случайную величину Y, равную их сумме (Y = X₁ + Х₂ + …+ Х_n) и случайную величину Z, равную их среднему арифметическому

тогда математическое ожидание их суммы равно сумме их математических ожиданий

(1)

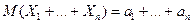
дисперсия суммы равна

(2)

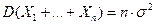
математическое ожидание среднего арифметического равно

(3)

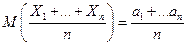
дисперсия среднего арифметического равна

(4)

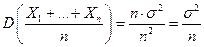
Частные случаи: если a₁ = a₂ = …= a_n , т.е все математические ожидания одинаковы, то

(1а)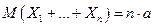

(3а)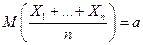

Замечания:

1. Формулы 1-4 следуют из свойств математического ожидания и дисперсии.

2. из формулы 4 следует, что дисперсия среднего арифметического случайных величин в n раз меньше, чем дисперсия каждого из слагаемых, поэтому для уменьшения ошибки рекомендуется использовать среднее арифметическое.