Теорема умножения вероятностей.
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, т.е.
(10) 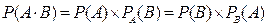 для двух зависимых событий;
для двух зависимых событий;
Для нескольких попарно зависимых событий А1,А2,…Аn:
(11) 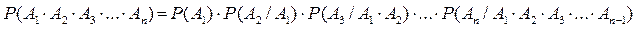
Для независимых событий теорема умножения вероятностей согласно (9) представлена формулой
(12) 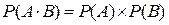 .
.
Пример:
В ящике имеется 10 электрических лампочек из которых 3 неисправны. На удачу одну за другой вынимают 2 лампочки.
А) какова вероятность, что обе исправны.
Б) какова вероятность, что обе неисправны.
В) какова вероятность, что одна из двух исправна.
Г) какова вероятность, что хотя бы одна исправна.
Решение: Обозначим события М-1я-исправна; К-2я-исправна
События М и К зависимые (т.е. вероятность события К меняется от того, произошло событие М или нет)
А) 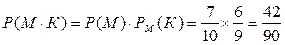
Б) 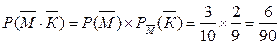
В) "первая хорошая, вторая плохая илипервая плохая, вторая хорошая"
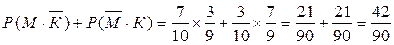
Г) "хотя бы одна исправна, т.е. одна или больше ( ≥ 1), первая исправна или вторая исправна
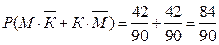
Замечание: Если вопрос задачи звучит как "хотя бы", то часто удобнее перейти к противоположному событию, т.е. "хотя бы одна исправная = 1 – Р (обе неисправны)"
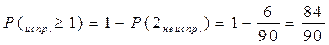
Пример:
Бросаем 2 монеты. Событие А – 2 герба, событие В – 2 решки, событие С – 1 герб и 1 решка. Являются ли равновозможными события? Результаты для каждой из монет независимы.
Решение:
А) 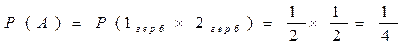
Б) 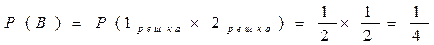
В) "герб и решка или решка и герб"
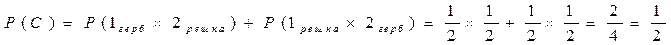
Формула полной вероятности и формула Байеса.
Пример:
Однотипная продукция выпускается 3-мя цехами, производительности которых относятся как 1:3:2. Вероятность брака в каждом цехе составляет соответственно 1, 2 и 3%. Все изделия хранятся на одном складе. Наудачу одно изделие выбирается на складе. Какова вероятность, что оно браковано.
Решение:
I – A1 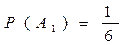
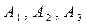 составляют полную группу
составляют полную группу
II – A2 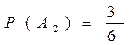
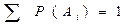
III – A3 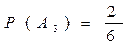
E – бракованное изделие
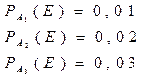
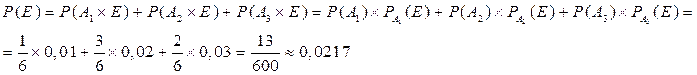
Пусть событие Е может произойти с любым из событий A1, A2, и т.д., образующих полную группу. Тогда полная вероятность события Е определяется формулой:
(12) 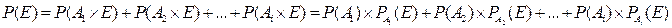
Пусть в условиях предыдущего примера известно, что наудачу взятое изделие оказалось бракованным.
А) какова вероятность, что оно было сделано в первом цеху.
Б) если известно, что изделие браковано, в каком цеху вероятнее всего было сделано.
Ответ на поставленный вопрос (переоценка гипотез при дополнении информации) дают формулы Байеса.
(13) 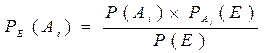
Доказательство:
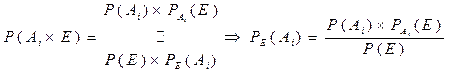
Выражая неизвестную величину через известные, получаем формулу 13, что и требовалось доказать.
С помощью формулы 13 отвечаем на вопрос задачи.
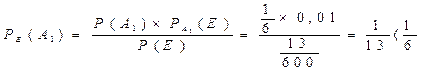
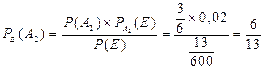
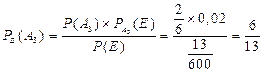
Значит, вероятнее всего бракованное изделие будет сделано впервом или втором цеху.
Дата добавления: 2015-05-26; просмотров: 945;
