Интегральная теорема Муавра-Лапласа
Вспомним: 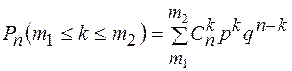
Переходя к пределу, при 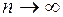 , заменяем
, заменяем 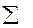 ,
, 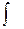 получим:
получим:
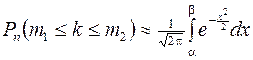 , (9)
, (9)
где 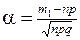 ;
; 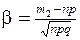 .
.
Для вычислении
я по этой формуле вводится функция Лапласа (интеграл вероятности):
 , (10)
, (10)
обладающая следующими свойствами:
а) 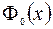 – нечетная функция; б)
– нечетная функция; б) 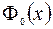 – возрастает на R;
– возрастает на R;
в) 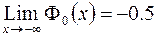 ; г)
; г) 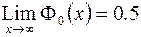 .
.
Учитывая свойства функции Лапласа, окончательно получим:
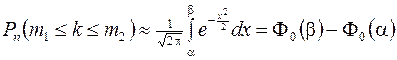 .
.
Теорема Пуассона (Закон редких событий)
Пусть у нас n1 – число опытов; p – вероятность успехов, 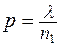 . В случае n2 > n1 считаем, что
. В случае n2 > n1 считаем, что 
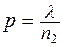 . Пусть при
. Пусть при 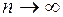 ,
, 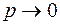 , тогда по известной формуле оценим вероятность ровно k – успехов в схеме Бернулли:
, тогда по известной формуле оценим вероятность ровно k – успехов в схеме Бернулли:
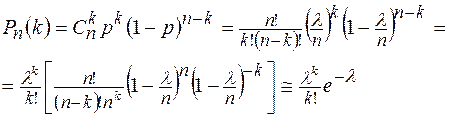
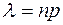 – среднее значение.
– среднее значение.
Если требовать, чтобы: 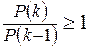 ,
, 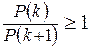 ,
, 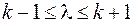
Если n – велико, а вероятность р – мала, то при npq < 10 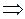 Пуассон, иначе ЛТМЛ.
Пуассон, иначе ЛТМЛ.
ПРИМЕР 1: Производится 4 независимых выстрела с вероятностью попадания р = 0.25. Какова вероятность событий: Р4(0), Р4(1), Р4(2), Р4(3), Р4(4)?
РЕШЕНИЕ: 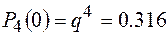 .
. 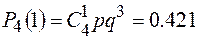 .
.
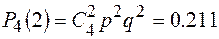 .
. 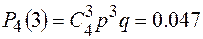 .
.
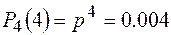
ПРИМЕР 2: Вероятность появления бракованной детали р = 0.005. Какова
вероятность того, что в партии из 10000 деталей бракованных будет не более 70?
РЕШЕНИЕ: Схема испытаний Бернулли:
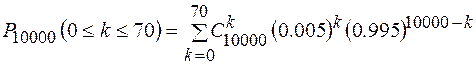
Вспомним интегральную теорему Муавра–Лапласа:
здесь m1 = 0; m2 = 70. Находим:
m1 – np =-50, m2 – np = 20.
 ,
, 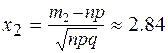 .
.
Окончательно получим: 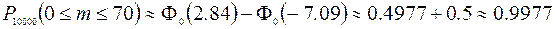 .
.
Дата добавления: 2015-06-10; просмотров: 1046;
