Найти вероятность того, что некто подойдет и из произвольной урны вынимает белый шар?

Решение: рассмотрим 3 гипотезы:

Н₁ – выбор 1 урны;

Н₂ – выбор 2 урны;

Н3 – выбор 3 урны.

Событие А – появление белого шара. Т.к. по условию задачи гипотезы равновозможны, то Р(Н₁) = Р(Н₂) = Р(Н₃) = 1 / 3. Условные вероятности события А при этих гипотезах соответственно равны: Р(А/Н₁) = 2 / 3; Р(А/Н₂) = 3/4;
Р(А/Н₃) = 1/2. По формуле полной вероятности получим:

.

Решение: как видно из рисунка, странник обязательно проходит через один из пунктов В₁, В₂, В₃ и В₄. Обозначим Н_k – гипотезы, состоящие в том, что путник при своем движении попадет в пункт В_k. Очевидно, что события Н₁, Н₂, Н₃ и Н₄ – образуют полную группу событий. Очевидно, что эти гипотезы (события) равновероятны, т.к. по условию, странник наугад выбирает один из путей ОВ₁, ОВ₂, ОВ₃ или ОВ₄. Тогда Р(Н_k) = 1/4. Из пункта В₁ в А можно прийти лишь по одному из трех равновероятных направлений. Так что условная вероятность достичь А при условии Н₁ равна 1/3. Т.е. Р(А/Н₁) = 1/3; Р(А/Н₂) = 1/2; Р(А/Н₃)=1; Р(А/Н₄) = 2/5. По формуле полной вероятности:

Р(А) = 1/4 (1/3 + 1/2 + 1 + 2/5) = 67/120.

Теорема гипотез

(Формула Байеса)

Следствием теоремы умножения и формулы полной вероятности является теорема гипотез, или формула Байеса.

Поставим задачу.

Имеется полная группа несовместных гипотез Н₁, Н₂,..., Н_n. Вероятности этих гипотез известны и составляют соответственно Р(Н₁), Р(Н₂),..., Р(Н_n). Произведен опыт, в результате которого наблюдалось событие А. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события?

Фактически здесь необходимо найти условную вероятность Р(Н_i/А) для каждой гипотезы. Из теоремы умножения вероятностей имеем:

Р(А Н_i) = Р(А) Р(Н_i/А) = Р(Н_i) Р(А/Н_i) (i = 1, 2,..., n).

Отсюда: Р(А) Р(Н_i/А) = Р(Н_i) Р(А/Н_i) (i = 1, 2,.. , n).

Окончательно получим: Р(Н_i/А) = 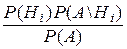(i = 1, 2,..., n).

Выражая Р(А) с помощью формулы полной вероятности получим:

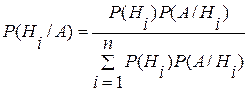(i = 1, 2,..., n) – формула Байеса.

ПРИМЕР 3: прибор может собираться из высококачественных деталей и из деталей обычного качества. 40 % приборов собирается из высококачественных деталей и их надежность за время t равно 95 %. Приборы из обычных деталей за время t имеют надежность 0.7. Прибор испытан и за время t работал безотказно. Какова вероятность того, что он собран из высококачественных деталей?

Решение: возможны 2 гипотезы:

Н₁ – прибор собран из высококачественных деталей;

Н₂ – прибор собран из некачественных деталей.

Вероятность этих гипотез до опыта: Р(Н₁) = 0.4, Р(Н₂) = 0.6.

В результате опыта наблюдалось событие А – прибор безотказно работал время t. Условные вероятности этого события при гипотезах Н₁ и Н₂ равных: Р(А/Н₁) = 0.95, Р(А/Н₂) = 0.7

По формуле Байеса находим вероятность гипотеза Н₁:

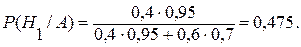
ПРИМЕР 4: в урне содержится три шара белого и черного цвета, причем распределение числа шаров по цветам неизвестно. В результате испытания из урны извлекли 1 шар. а) Сформулировать гипотезы о содержимом урны до испытания и указать их вероятности. б) Найти вероятности гипотез после испытания, состоящего в извлечении из урны белого шара.

Решение:

а) До испытания выскажем четыре попарно несовместимых и равновероятных гипотезы:

1) Н₁ – в урне 3 белых и 0 черных шаров;

2) Н₂ – в урне 2 белых и 1 черных шаров;

3) Н₃ – в урне 1 белых и 2 черных шаров;

4) Н₄ – в урне 0 белых и 3 черных шаров;

Р(Н₁) = Р(Н₂) = Р(Н₃) = Р(Н₄) = ¼.

б) Т.к. извлечен белый шар, то Р(А/Н₄) = 0, Р(А/Н₃) = 1/3, Р(А/Н₂) = 2/3, Р(А/Н₁) = 1.

По формуле Байеса: