Повторение испытаний
(Схема Бернулли)
Если производится несколько испытаний (опытов), причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В схеме Я. Бернулли рассматривается серия, состоящая из n независимых испытаний, каждое из которых имеет лишь две исхода: наступление какого-то события А (успех) или его не наступление (неудача). Причем вероятность успеха при одном испытании равна Р(А) = р (0 ≤ p ≤ 1) – постоянна и не зависит от номера испытаний. Следовательно, вероятность неуспеха Р( 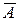 )=1 – p = q – тоже постоянна.
)=1 – p = q – тоже постоянна.
Поставим своей задачей вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится n – k раз.
По теореме умножения вероятностей получим:
p·p·....·p·q·q·....·q = pk qn-k
K n-k
 |  |




 А А А А ...................A A A A A ...................... A
А А А А ...................A A A A A ...................... A
 |
N
Число возможных вариантов выборки k элементов из n вычисляется по формуле:
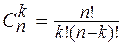 .
.
Окончательно получим:
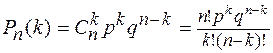 (1)
(1)
Это и есть формула Бернулли (Биномиальное распределение). Вспомним формулу бинома Ньютона:
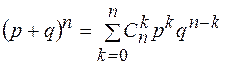 (2)
(2)
Отсюда, и непосредственно из формулы Бернулли (1) следует:
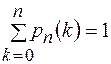 (3)
(3)
Очевидно этот же результат получится, если вспомнить, что для
k = {0, 1, 2, ...., n} – получим полную группу событий, вероятность которой равна 1.
Введем обозначения, пусть 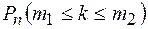
 означает вероятность того, что в n испытаниях схемы Бернулли успех наступит не менее чем
означает вероятность того, что в n испытаниях схемы Бернулли успех наступит не менее чем
m1 – раз, и не более, чем m2 – раз ( 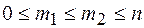 ). Тогда имеет место формула:
). Тогда имеет место формула:
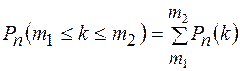 (4)
(4)
Вероятность 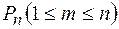 того, что в результате n испытаний, успех наступит хотя бы 1 раз, определяется формулой:
того, что в результате n испытаний, успех наступит хотя бы 1 раз, определяется формулой:
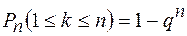 (5)
(5)
Необходимо найти k0 – наивероятнейшее число успехов, т.е. такое k0 вероятность которого максимальна.
Запишем условия:
a) 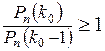 ; b)
; b) 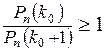 ;
;
а) 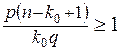 ;
; 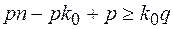 ;
; 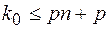 .
.
b) 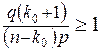 ;
; 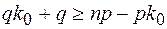 ;
; 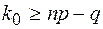 .
.
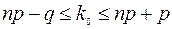 . (6)
. (6)
При n → ∞ (достаточно большом) получим 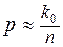 – (вспомним частотное определение вероятности).
– (вспомним частотное определение вероятности).
Значит, можно сказать, что при больших n наиболее вероятная частота успеха совпадает (равна) вероятности успеха при одном испытании.
ПРИМЕР: Вероятность того, что расход электроэнергии на продолжении одних суток не превышает установленной нормы, равна р=0.75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
РЕШЕНИЕ: Вероятность нормального расхода р=0.75. Вероятность перерасхода q=0.25. Искомая вероятность по формуле Бернулли:
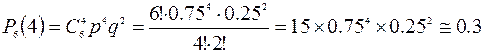 .
.
Рассмотрим обобщение схемы Бернулли.
Производим n независимых испытаний, каждое из которых имеет m (m > 2) попарно несовместимых и единственно возможных исходов Аj(j = 1, 2, ..., m). Т.е. Аj – полная группа событий. Вероятности наступления каждого события pi = P(Ai) – в общем случае различны и удовлетворяют условию 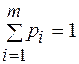 . В этих условиях для произвольно заданных целых неотрицательных чисел ki таких, что
. В этих условиях для произвольно заданных целых неотрицательных чисел ki таких, что 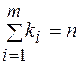 выводится вероятность Pn(k1, k2, .., km) того, что при n испытаниях исход А1 наступит ровно k1 раз, исход
выводится вероятность Pn(k1, k2, .., km) того, что при n испытаниях исход А1 наступит ровно k1 раз, исход 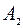 – k2 раз и т.д., исход Am произойдет km раз:
– k2 раз и т.д., исход Am произойдет km раз:
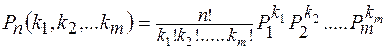 (7)
(7)
Это и есть полиномиальное распределение.
Дата добавления: 2015-06-10; просмотров: 1303;
