Р(А/В) Р(А).
Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
Р(АВ) = Р(А) Р(В/А) = P(B) P(A/B)
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.
Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
ПРИМЕР 3:
Прибор работающий в течение времени t, состоит из трех узлов, каждый из которых, независимо от других может в течение времени t отказать. Отказ хотя бы одного узла приводит к отказу прибора. За время t вероятность безотказной работы узлов соответственно равны: р1=0.8, р2=0.9, р3=0.7. Какова надежность прибора (вероятность безотказной работы) за время t?
Решение:
А – безотказная работа прибора
А1 – безотказная работа 1 узла
А2 – безотказная работа 2 узла
А3 – безотказная работа 3 узла
А = А1 А2 А3
Тогда по теореме умножения вероятностей независимых событий:
Р(А) = Р(А1) Р(А2) Р(А3) = р1 р2р3 = 0.504
ПРИМЕР 4:
Экзаменующимся по теории вероятностей было предложено 34 билета. Студент дважды извлекает по одному билету из предложенных (не возвращая их). Какова вероятность того, что студент сдаст экзамен, если он подготовил лишь 30 билетов и в первый раз вынул «неудачный» билет?
Решение:
Испытание состоит в том, что два раза подряд извлекают по одному билету, причем вынутый в первый раз билет назад не возвращается. Пусть событие А – "в первый раз вынут "неудачный" билет", В – "во второй раз вынут "удачный" билет". Очевидно, что события А и В зависимы, т.к. извлеченный в первый раз билет не возвращается в число всех билетов. Требуется найти вероятность события А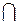 
В. По формуле:
Р(А 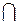В) = Р(А) Р(В/А);
Р(А) = 4/34; Р(В/А) = 30/33, тогда Р(А 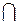В) = 
.
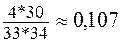Формула полной вероятности
Дата добавления: 2015-06-10; просмотров: 1029;