Закон сложения вероятностей

Рассмотрим несовместные события А₁, А₂ и их объединения А = А₁ 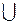А₂. Допустим происходит серия одинаковых и независимых между собой опытов, результатом каждого из которых могут быть указанные события А, А₁ или А₂. Пусть n – число всех испытаний, n(А), n(А₁) и n(А₂) – число тех из них, которые привели к наступлению соответствующих событий: А, А₁, А₂. Если в каком-то опыте произошло событие А, то это значит, что произошло или событие А₁ или событие А₂ (одновременно А₁ и А₂ произойти не могут, так как по условию они несовместны). Поэтому числа n(А), n(А₁) и n(А₂) связаны соотношением:

n(А) = n(А₁) + n(А₂) (1)

Следовательно, частоты рассматриваемых событий таковы, что

n(А) / n = n(А₁) / n + n(А₂) / n (2)

При достаточно большом числе испытаний n частоты практически совпадают с соответствующими вероятностями. Так что соответствующие вероятности будут связаны между собой равенством:

P(А) = P(А₁) + P(А₂)(3)

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Обобщив эту теорему на любое число несовместных событий, получим:

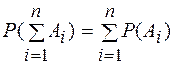(4)

Следствие 1. Если события А1, А2,....Аn образуют полную группу попарно несовместных событий, то сумма их вероятностей равна 1:

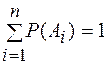. (5)

Противоположными событиями называются два несовместных события, составляющие (образующие) полную группу. А и .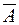

Примеры противоположных событий:

1. А – попадание при выстреле;

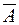– промах при выстреле.

2. С – при бросании кубика выпала 6;

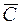– при бросании кубика 6 не выпала.

Следствие 2. Сумма вероятностей противоположных событий равна 1:

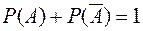. (6)

ПРИМЕР:

В лотерее 1000 билетов: из них на один билет падает выигрыш 500 рублей, на 10 билетов – выигрыши по 100 рублей, на 50 билетов выигрыши по 20 рублей, на 100 билетов – выигрыши по 5 рублей, остальные билеты - не выигрышные. Некто покупает один билет. Найти вероятность выиграть не менее 20 рублей.

Решение:

А – выигрыш не менее 20 рублей

А₁ – выигрыш 20 рублей

А₂ – выигрыш 100 рублей

А₃ – выигрыш 500 рублей

Очевидно: А = А₁ + А₂ + А₃

По теореме сложения вероятностей:

Р(А) = Р(А₁) + Р(А₂) + Р(А₃) = 0.050 + 0.010 + 0.001 = 0.061.

Как было указано выше, теорема сложения вероятностей справедлива только для несовместных событий. В случае, когда события А и В – совместны, вероятность суммы этих событий выражается формулой:

Р(А + В) = Р(А) + Р(В) – Р(АВ). (7)

Аналогично запишем вероятность суммы трех совместных событий:

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) – Р(АВС) (8)

Справедливость формул (7) и (8) наглядно иллюстрируются рисунками:

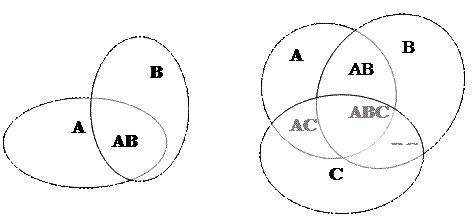Аналогичную формулу можно написать для произведения событий. Действительно, как следует из рисунка:

Р(АВ) = Р(А) + Р(В) – Р(А + В) (9)