Элементы комбинаторики
Правило произведения. Если компоненту х1 строки (х1, х2,....,хк) можно выбрать n1 способами и после каждого такого выбора х1 компоненту х2 можно выбрать n2 – способами. После выбора х1 и х2 компоненту х3 можно выбрать n3 способами и т.д., наконец хк независимо от выбора всех предыдущих компонент можно выбрать nk способами. Тогда количество возможностей (комбинаций) образования строки (х1, х2,....,хк) равно:
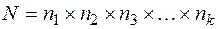 . (1)
. (1)
ПРИМЕР 1: Обед в университетской столовой состоит из трех блюд. Первое блюдо в меню может быть выбрано 5 способами, второе блюдо - 4, а третье блюдо - 3. Сколько дней студент может съедать новый обед, если любая комбинация блюд возможна, и один обед от другого должен отличаться хотя бы одним блюдом?
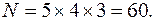
Правило суммы. Если множество Е1 содержит n1 элемент, множество Е2 - n2 элементов, ..., и множество Ек - nk элементов. И если эти множества попарно не пересекаются, то число элементов в их объединении равно сумме чисел элементов, содержащихся в каждом из этих множеств:
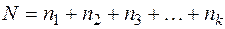 . (2)
. (2)
Перестановки. Пусть Е(n)={x1, x2,....,xn} – произвольное (неупорядоченное) n – элементное множество. Рассмотрим различные комбинации его упорядочивания. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком следования входящих в них элементов, и называются перестановками из n – элементов. Число всех таких перестановок обозначается символом Pn и находится по формуле:
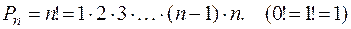 . (3)
. (3)
ПРИМЕР 2: Пятеро гостей случайным образом рассаживаются за столом. Сколькими способами можно их рассадить так, чтобы хотя бы 2 гостя поменялись местами (изменился порядок)?
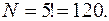
Размещения. Различные упорядоченные m – элементные подмножества данного неупорядоченного множества E(n) (m < n) называются размещениями из n элементов по m. Число таких размещений обозначается 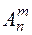 и вычисляется по формуле:
и вычисляется по формуле:
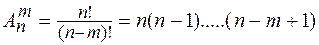 . (4)
. (4)
ПРИМЕР 3: Десять участников финала разыгрывают одну золотую, одну серебряную и одну бронзовую медали. Сколькими способами эти награды могут быть распределены между спортсменами?
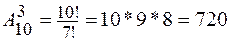 .
.
Сочетания. Различные неупорядоченные m – элементные подмножества множества E(n) (m < n) называются сочетаниями из n элементов по m. Число всех таких сочетаний обозначается символом 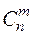 и определяется по формуле:
и определяется по формуле:
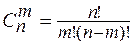 . (5)
. (5)
ПРИМЕР 4: В полуфинальном забеге участвуют десять спортсменов. Три спортсмена, показавших лучший результат, попадают в финал. Сколько существует различных троек финалистов?
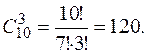
Примечания:
Размещения из n – элементов по m представляют собой такие m – элементные выборки из множества Е(n), которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.
Сочетания же из n – элементов по m представляет собой m – элементные выборки, отличающиеся только самими элементами.
Размещения с повторениями. Любая строка длиной m, составленная из элементов множества Е(n), называется размещением с повторением из n – элементов по m. Число всех размещений с повторениями обозначается символом 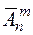 и вычисляется по формуле:
и вычисляется по формуле:

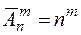 . (6)
. (6)
ПРИМЕР 5: Для автомобильных номеров используются 10 цифр и 28 букв. Каждый номер состоит из 3 букв и 4 цифр. Какое максимальное число машин может получить номера при такой системе нумерации?
РЕШЕНИЕ: Сначала осуществим выбор 4 цифр. Каждый такой комплект цифр представляет собой четырехэлементную выборку из 10 – элементного массива цифр, т.е. является размещением с повторениями из 10 элементов по 4. Следовательно, общее число таких элементов равно 104. Исключим из выборки 00-00. Аналогично выбор трех букв из 28 осуществляется 283 числом способов. Т.к. номер каждой машины есть упорядоченная "пара", состоящая из комплекта цифр и комплекта букв, то по правилу произведения число всех номеров будет равно N = (104-1)*283 = 219 498 048.
Пространство элементарных событий. Случайные события.
Под событием в теории вероятностей понимается всякий факт, который в результате опыта может произойти или не произойти.
Примеры событий:
А – появился герб при бросании монеты;
В – появление трех гербов при трехкратном бросании монеты;
С – попадание в цель при выстреле;
D – появление туза при вынимании карты из колоды; и т.д.
Рассматривая вышеперечисленные события, мы видим, что каждое из них обладает какой-то степенью возможности: одни – большей, другие – меньшей. Причем, для некоторых событий мы сразу же можем решить, какое из них более, а какое менее возможно. Чтобы количественно сравнить между собой события по степени их возможности, очевидно нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое число мы называем вероятностью события.
Рассмотрим множество событий М, которые можно наблюдать в некотором эксперименте. Выделим, прежде всего, два специальных события – достоверное событие - U, которое обязательно происходит в эксперименте, и невозможное событие - V, которое не может произойти в эксперименте никогда.
Для каждого события А из М введем противоположное событие 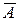 , которое состоит в том, что событие А не произошло.
, которое состоит в том, что событие А не произошло.
Событие А + В (А 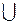 В), заключающееся в том, что из двух событий А и В происходит по крайней мере одно (либо А, либо В, либо А и В вместе), называется суммой (или объединением) событий А и В.
В), заключающееся в том, что из двух событий А и В происходит по крайней мере одно (либо А, либо В, либо А и В вместе), называется суммой (или объединением) событий А и В.
Событие АВ (А 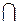 В), заключающееся в том, что события А и В происходят одновременно, называется произведением (или пересечением) событий А и В.
В), заключающееся в том, что события А и В происходят одновременно, называется произведением (или пересечением) событий А и В.
Событие А \ В называется разностью событий А и В; оно заключается в том, что происходит А и не происходит В.
Предположим, что среди всех возможных событий А, которые в данном опыте по воле случая происходят или не происходят, можно выделить совокупность так называемых элементарных событий или элементарных переходов, обладающих следующими свойствами:
во-первых, все они взаимоисключают друг друга, т.е. являются непересекающимися;
во-вторых, в результате данного опыта обязательно происходит одно из этих элементарных событий;
в-третьих, каково бы ни было событие А, по наступившему элементарному исходу всегда можно судить о том, происходит или не происходит это событие.
Элементарные исходы обычно обозначаются греческой буквой 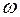 , а их совокупность
, а их совокупность 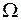 называется пространством элементарных событий.
называется пространством элементарных событий.
ПРИМЕР 1: При бросании двух игральных костей элементарным исходом можно считать пару чисел 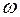 =(a, b), где а – число очков на первой кости, b – число очков на второй кости. При этом (1
=(a, b), где а – число очков на первой кости, b – число очков на второй кости. При этом (1 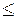 a, b
a, b 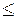 6).
6).
ПРИМЕР 2: Сделано 5 выстрелов по мишени. Элементарным исходом данного опыта является: 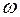 = а, где а – число (0 £ а £50).
= а, где а – число (0 £ а £50).
Рассмотрим геометрическую интерпретацию возможных событий:
a) | b) | c) | a) D = A È B; b) D = A È B; c) D = A È B; |
г) А=А1 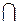 А2;
А2;
д) А=А1\А2;
е) А=А2= 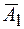 .
.
Здесь каждой картинке (прямоугольнику) соответствует пространство элементарных событий 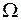 .
.
Два события А и В несовместимы (или несовместны), если А 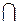 В = Æ
В = Æ
(т.е. событие невозможно).
События Е1, Е2,..., Еn – образуют полную группу событий, если они попарно несовместны и:
Е1 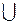 Е2
Е2 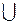 Е3
Е3 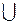 ...
... 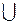 Еn =
Еn = 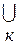 Ек = Ек, т.е. из этих событий происходит одно и только одно.
Ек = Ек, т.е. из этих событий происходит одно и только одно.
Таким образом, пусть 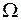 - пространство элементарных переходов
- пространство элементарных переходов 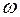 рассматриваемого опыта или явления. Для каждого, связанного с этим опытом события А можно выделить совокупность тех элементарных переходов
рассматриваемого опыта или явления. Для каждого, связанного с этим опытом события А можно выделить совокупность тех элементарных переходов 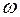 , наступление которых влечет за собой наступление события А. Обозначим множество (совокупность) этих элементарных переходов
, наступление которых влечет за собой наступление события А. Обозначим множество (совокупность) этих элементарных переходов 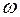 тем же символом А, что и соответствующее событие А.
тем же символом А, что и соответствующее событие А.
Очевидно событие А наступает тогда и только тогда, когда наступает один из элементарных переходов 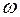 , входящих в указанное множество А. Другими словами, событие А равно событию, которое состоит в том, что наступает какой либо элементарный переход
, входящих в указанное множество А. Другими словами, событие А равно событию, которое состоит в том, что наступает какой либо элементарный переход 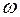 , входящий в множество А (
, входящий в множество А ( 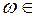 А). Т.е. событие А можно отождествить с множеством А элементарных переходов
А). Т.е. событие А можно отождествить с множеством А элементарных переходов 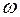 .
.
Достоверное событие А, наступающее в результате любого из элементарных переходов 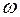 , при таком отождествлении событий множеств совпадает с пространством
, при таком отождествлении событий множеств совпадает с пространством 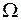 : А =
: А = 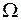 .
.
Невозможное событие А, не наступающее ни при каком элементарном переходе 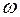 , совпадает с пустым множеством и обозначается А = Æ.
, совпадает с пустым множеством и обозначается А = Æ.
Вероятность
Испытаниемназывается эксперимент, который можно (хотя бы принципиально) провести в одинаковых условиях любое число раз. Простейший результат испытания называется элементарным событием или исходом. При испытании неизбежно наступает какой-то исход и только один.
Если событие может привести кn различным равновозможным исходам и если вm случаях появится признакА,то частота (вероятность) события А обозначается r(A) и равна отношению m к n, то есть
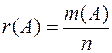 . (1)
. (1)
Это так называемое частотное (комбинаторное) определение вероятности.
Событие А, для которого частота r(A) при достаточно больших n мало отличается от некоторого фиксированного числа, не зависящего от серии проводимых испытаний, называется статически устойчивым.
Вероятностью статически устойчивого случайного события А называется число Р(А), около которого группируются частоты этого события в длинных сериях независимых испытаний:
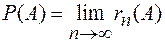 . (2)
. (2)
Пример1. При подбрасыванием идеальной монеты вероятность появления герба в каждом отдельном испытании равна Р(А) = 1\2. Ниже в таблице приведены результаты длинных серий опытов.
| Экспериментатор | n | m(А) | rn(А) |
| Ж.Л.Л. Бюррон | 0,5069 | ||
| К. Пирсон | 0,5016 | ||
| К. Пирсон | 0,5005 |
ПРИМЕР 2: Имеется колода тщательно перемешанных карт (36 листов). Наугад вытаскивается одна карта. Сколько, в среднем, надо провести опытов, чтобы этой картой был туз пиковый?
Решение. Так как в колоде только одна карта туз пиковый, то частота (вероятность) появления туза пикового равна 1/36. Вспомним, что r(A) = m / n. Отсюда n = m / r(A), в нашем случае m = 1, тогда n = 36.
Современное понятие вероятности
Введем пространство 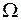 , элементы которого е1, е2, .... назовем элементарными событиями. Определим в нем неотрицательную меру, называемую вероятностью со свойствами:
, элементы которого е1, е2, .... назовем элементарными событиями. Определим в нем неотрицательную меру, называемую вероятностью со свойствами:
1. Р( 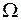 ) = 1, т.е. вероятность того, что наблюдаемое событие принадлежит к числу тех, которые могут наблюдаться, равно единице.
) = 1, т.е. вероятность того, что наблюдаемое событие принадлежит к числу тех, которые могут наблюдаться, равно единице.
2. Если множество элементарных событий А и В не имеют общих элементов , то 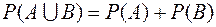 , т.е. вероятность того, что событие принадлежит либо множеству А, либо множеству В, равно сумме вероятностей обнаружить событие отдельно в множестве А и множестве В.
, т.е. вероятность того, что событие принадлежит либо множеству А, либо множеству В, равно сумме вероятностей обнаружить событие отдельно в множестве А и множестве В.
Рассмотрим теперь следствие, которое служит примером использования этих аксиом. Пусть 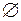 - пустое множество событий, иначе говоря,
- пустое множество событий, иначе говоря, 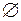 означает отсутствие событий. Тогда (
означает отсутствие событий. Тогда ( 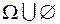 ) =
) = 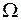 и
и 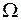 не имеет общих элементов с
не имеет общих элементов с 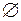 .
.
Следовательно:
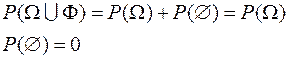 (3)
(3)
Дата добавления: 2015-06-10; просмотров: 2197;