Соответствие между возможными значениями СВ и вероятностями этих значений называют распределением вероятностей СВ и обозначают .
Законом распределения СВ называется всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
Тогда о СВ можно говорить, что она подчинена данному закону. Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения СВ и соответствующие им вероятности.
| xi | x1 | x2 | .... | xn |
| pi | p1 | p2 | .... | pn |
Такую таблицу будем называть рядом распределения СВ.
Чтобы придать ряду распределения более наглядный вид часто прибегают к его графическому отображению.

Такая фигура называется многоугольником распределения.
ПРИМЕР 1: Стрелок ведет стрельбу по мишени до первого попадания, имея боезапас 4 патрона. Вероятность попадания при каждом выстреле равна 0.6. Построить ряд распределения боезапаса, оставшегося неизрасходованным.
РЕШЕНИЕ: СВ Х – число неизрасходованных патронов имеет четыре возможных значения: 0, 1, 2 и 3. Вероятности этих значений равны соответственно:p0 = 0.43 = 0.064, p1=0.42·0.6 = 0.096, p2 = 0.4·0.6 = 0.24, p3 = 0.6.
| xi | ||||
| pi | 0.064 | 0.096 | 0.24 | 0.6 |
Очевидно, что ряд распределений не универсальная характеристика. Нетрудно убедиться, что для непрерывной СВ такую характеристику построить нельзя (т.к. СВ имеет бесчисленное множество значений). Поэтому составить таблицу, в которой бы были перечислены все возможные значения СВ невозможно. Кроме того, как мы убедимся в дальнейшем, каждое отдельное значение непрерывной СВ обычно не обладает никакой, отличной от нуля, вероятностью.
Однако различные области возможных значений СВ все же не являются одинаково вероятными и для непрерывной СВ существует "распределение вероятностей", хотя и не в том смысле, как для дискретной.
Для количественного описания этого распределения вероятностей удобно воспользоваться не вероятностного события Х = х, а вероятностью события Х < х, где х - некоторая текущая переменная. Вероятность этого события, очевидно, зависит от х, и является некоторой функцией от х. Эта функция называется функция распределения случайной величины Х и обозначается F(x).
F(x) = P(X < x) (6.3)
Функцию F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.
Функция распределения – самая универсальная характеристика СВ. Она существует как для дискретных, так и непрерывных СВ. Функция распределения полностью характеризует СВ с вероятностной точки зрения, т.е. является одной из форм закона распределения.
Укажем некоторые общие свойства функции распределения:
1. Функция распределения F(x) неубывающая функция своего аргумента, т.е. при х2 > х1 F(x2) 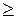 F(x1).
F(x1).
2. На минус бесконечности функция распределения равна нулю: 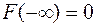 .
.
3. На плюс бесконечности функция распределения равна единице: 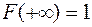 .
.
4. 
График функции распределения в общем случае представляет собой график неубывающей функции, значение которой начинается от 0 и доходит до 1, причем в отдельных точках функция может иметь разрыв.
Зная ряд распределения дискретной СВ, можно легко построить функцию распределения этой величины.
Действительно: 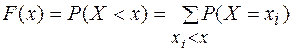 .
.
ПРИМЕР 2: Произведем один опыт, в котором может произойти или не произойти событие А. Вероятность события А р = 0.3. СВ Х – число появлений события А в опыте (дискретная СВ). Необходимо построить функцию распределения СВ.
РЕШЕНИЕ: Ряд распределения СВ Х имеет вид:
| xi | ||
| pi | 0.7 | 0.3 |
Построим функцию распределения случайной величины Х:
1. при х 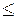 0 F(x) = P(X < x) = 0;
0 F(x) = P(X < x) = 0;
2. при 0 < x 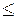 1 F(x) = P(X < x) = P(X = 0) = 0.7;
1 F(x) = P(X < x) = P(X = 0) = 0.7;
3. при x > 1 F(x) = P(X < x) = P(X = 0) + P(X = 1) = 1.
ПРИМЕР 3: При тех же условиях провели 4 независимых опыта. Постройте функцию распределения числа появлений события А.
РЕШЕНИЕ: Х – число появлений события А в 4 опытах. Эта величина имеет ряд распределения:
| xi | |||||
| pi | 0.2401 | 0.4116 | 0.2646 | 0.0756 | 0.0081 |
Построим функцию распределения СВ Х:
1. при 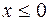 F(x) = 0;
F(x) = 0;
2. 0 < x 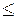 1 F(x) = 0.2401;
1 F(x) = 0.2401;
3. 0 < x 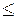 2 F(x) = 0.6517;
2 F(x) = 0.6517;
4. 0 <x 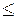 3 F(x) = 0.9163;
3 F(x) = 0.9163;
5. 0 < x 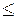 4 F(x) = 0.9919;
4 F(x) = 0.9919;
6. x > 4 F(x) = 1.
Дата добавления: 2015-06-10; просмотров: 1466;
