Пример 2. СВ подчинена закону распределения с плотностью
СВ 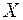 подчинена закону распределения с плотностью
подчинена закону распределения с плотностью

Необходимо: а) найти коэффициент  ; б) построить график плотности распределения
; б) построить график плотности распределения  ; в) найти
; в) найти 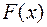 и построить график; г) найти вероятность попадания СВ
и построить график; г) найти вероятность попадания СВ 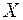 на участок
на участок  .
.
Решение а) 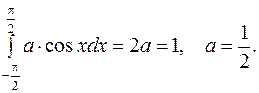
б)

в) По формуле (7.6) получим выражение для функции распределения:

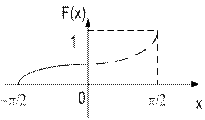
г) 
На практике в теории вероятностей применяют характеристики положения случайных величин, отражающие те или другие особенности распределения.
Модой  случайной величины
случайной величины 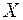 называется ее наиболее вероятное значение (для которого вероятность
называется ее наиболее вероятное значение (для которого вероятность 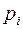 или плотность вероятности
или плотность вероятности 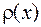 достигает максимума).
достигает максимума).
Если вероятность или плотность вероятности достигает максимума в одной точке, распределение называется унимодальным, если же максимум достигается в нескольких точках, распределение называется полимодальным (рис. 7.4).
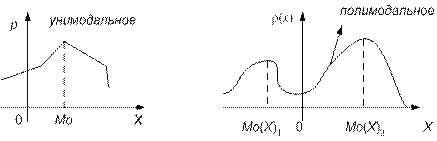
Рис.7.4. Мода распределения
Медианой 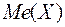 случайной величины
случайной величины 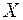 называется такое ее значение, при котором вероятность того, что СВ
называется такое ее значение, при котором вероятность того, что СВ  одинаково вероятна тому, что СВ
одинаково вероятна тому, что СВ  и будет равна 0.5.
и будет равна 0.5.
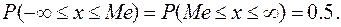 (7.9)
(7.9)
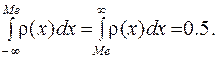 (7.10)
(7.10)
Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам (функция распределения равна 0.5) (рис. 7.5.).

Рис. 7.5. Медиана распределения
Квантилем уровня  (или
(или 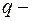 квантилем) называется такое значение
квантилем) называется такое значение  случайной величины, при котором функция ее распределения принимает значение, равное
случайной величины, при котором функция ее распределения принимает значение, равное  , т.е.
, т.е.
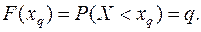 (7.10)
(7.10)
Некоторые квантили получили особое название. Очевидно, что определенная выше медиана случайной величины есть квантиль уровня 0.5, т.е. 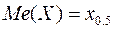 . Квантили
. Квантили 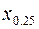 и
и 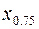 получили название соответственно верхнего и нижнего квартилей.
получили название соответственно верхнего и нижнего квартилей.
С понятием квантиля тесно связано понятие процентной точки. Под 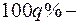 ной точкой подразумевается квантиль
ной точкой подразумевается квантиль 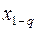 , т.е. такое значение случайной величины
, т.е. такое значение случайной величины 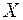 , при котором
, при котором 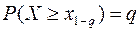 .
.
Дата добавления: 2015-06-10; просмотров: 1138;
