Свойства дисперсии

1. Дисперсия константы равна нулю:

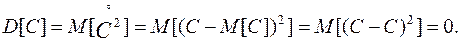(8.15)

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:

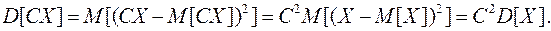(8.16)

3. Дисперсия алгебраической суммы конечного числа независимых СВ равна сумме их дисперсий. Покажем это свойство для двух СВ:

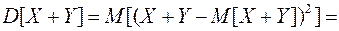
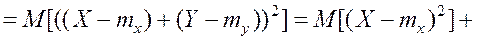
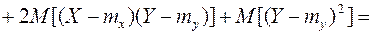
(8.17)

Учтем, что 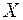и 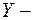независимые случайные величины, для которых выполняются свойства (8.5) и (8.10), т.е.:

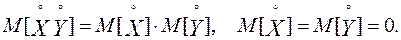(8.18)

С учетом (8.18) выражение (8.17) примет окончательный вид:

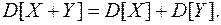(8.19)

Вычислим дисперсию разности СВ:

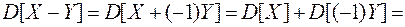
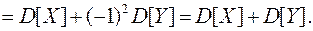(8.20)

4. Второй центральный момент случайной величины равен разности между вторым начальным моментом и квадратом первого начального момента этой случайной величины. Другими словами:

Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

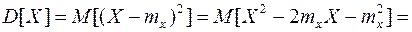
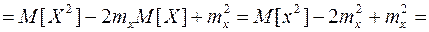
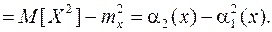(8.21)

5. Дисперсия произведения независимых СВ 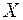и 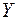равна произведению дисперсии 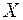на дисперсию 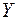плюс произведение квадрата математического ожидания СВ 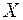на дисперсию 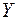плюс произведение квадрата математического ожидания СВ 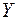на дисперсию 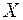. Покажем это:

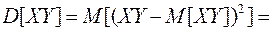
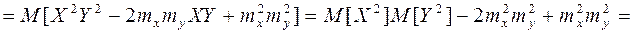
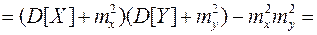
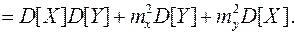(8.22)