Свойства двумерной функции распределения

1. Функция распределения 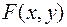есть неотрицательная функция, заключенная между нулем и единицей, т.е.

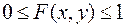. (9.3)

Это утверждение следует из того, что интегральная функция распределения двумерной СВ есть вероятность.

2. Функция распределения 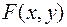есть неубывающая функция, по каждому из аргументов, т.е.

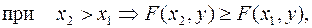
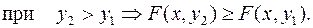(9.4)

Т.к. при увеличении какого-либо аргумента заштрихованная область на рис.9.1 увеличивается, то вероятность попадания случайной точки в эту область, по крайней мере, уменьшиться не может.

3. Если хотя бы один из аргументов обращается в 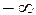, функция распределения 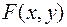равна нулю, т.е.

(9.5)

Функция распределения 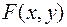в данных случаях равна нулю, т.к. события 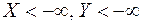и их произведение представляют невозможные события.

4. Если один из аргументов обращается в , функция распределения 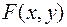становится равной одномерной функции распределения от другого аргумента:

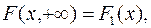
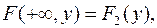(9.6)

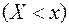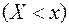где . Очевидность данного свойства (9.6) вытекает из того, что произведение события и достоверного события есть само событие , аналогично можно показать и для .

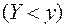5. Если оба аргумента равны , то функция распределения 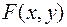равна единице:

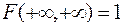. (9.7)

Это свойство обусловлено тем фактом, что совместная реализация двух достоверных событи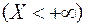й и есть событие достоверное, а вероятность достоверного события равна единице.

Рассмотрим вероятность попадания двумерной СВ в некоторый прямоугольник (см. рис. 9.2). Вероятность попадания случайной точки в указанный прямоугольник можно записать:

. (9.8)

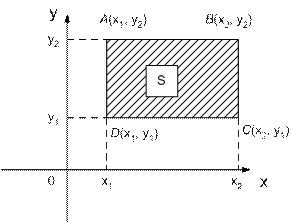
Рис.9.2. Вероятность попадания в прямоугольник

Зная функцию распределения 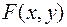, выразим искомую вероятность. Эта вероятность равна вероятности попадания в бесконечный квадрант с вершиной 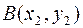, минус вероятности попадания в квадранты с вершинам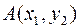и и 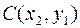плюс вероятность попадания в квадрант 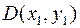(т.к. эта вероятность вычиталась дважды). Окончательно получим:

(9.9)