Плотность вероятности двумерной случайной величины

Двумерная случайная величина 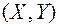называется непрерывной, если ее функция распределения 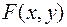- непрерывная функция, дифференцируемая по каждому из аргументов, и существует вторая смешанная производная .

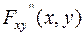Как и для одномерной случайной величины, введем понятие плотности вероятности двумерной СВ.

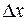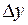Оценим вероятность попадания случайной точки в прямоугольник со сторонами и . Средняя плотность вероятности в данном прямоугольнике равна отношению вероятности к площади прямоугольника 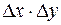. Будем неограниченно уменьшать стороны прямоугольника, устремив 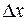и 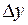к нулю. С учетом (9.9) получим:

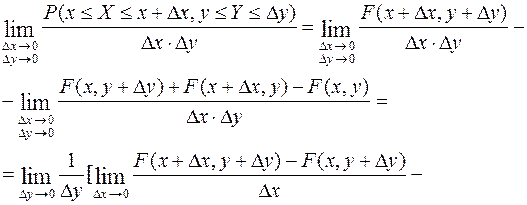
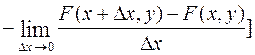(9.10)

Учитывая то, что функция непрерывна и дифференцируемая по каждому аргументу, выражение (9.10) примет вид:

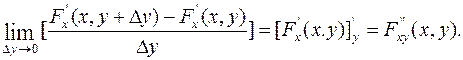(9.11)

Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины 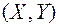называется вторая смешанная частная производная ее функции распределения, т.е.

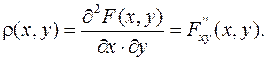(9.12)

Плотность распределения двумерной СВ обладает свойствами, аналогичными свойствам плотности вероятности одномерной СВ:

1. Плотность распределения двумерной случайной величины есть неотрицательная функция, т.е.

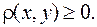(9.13)

Это свойство вытекает из того, что - функция неубывающая по каждому аргументу.

2. Вероятность попадания непрерывной двумерной случайной величины в область равна

(9.14)

По аналогии с одномерной СВ, для двумерной СВ введем понятие "элемент вероятности", равный 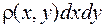. Он представляет (с точностью до бесконечно малых более высоких порядков) вероятность попадания случайной точки в элементарный прямоугольник со сторонами и 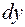. Тогда вероятность попадания двумерной СВ в область на плоскости 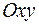геометрически изображается объемом цилиндрического тела, ограниченного сверху поверхностью распределения 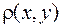и опирающегося на область , а аналитически – двойным интегралом (9.14).

3. Функция распределения непрерывной двумерной случайной величины выражается через ее плотность вероятности по формуле:

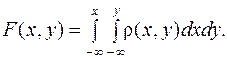(9.15)

Функция распределения есть вероятность попадания в бесконечный квадрант , который можно рассматривать как прямоугольник, ограниченный абсциссам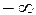и и 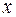и ординатам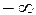и и .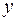

4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной СВ равен единице.

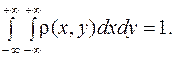(9.16)

Несобственный интеграл (9.16) есть вероятность попадания во всю плоскость 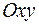, т.е. вероятность достоверного события, равная 1.

Зная плотность вероятности двумерной СВ 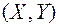можно найти функции распределения и плотности вероятностей ее одномерных составляющих и 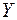. Учитывая (9.6) и (9.15), получим:

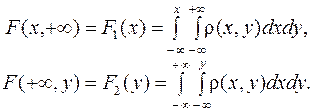(9.17)

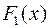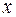Дифференцируя функции распределения и по аргументам и 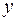соответственно, получим плотности вероятности одномерных СВ:

(9.18)

т.е. несобственный интеграл в бесконечных пределах от совместной плотности 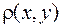двумерной случайной величины по аргументу 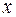дает плотность вероятности 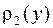, а по аргументу 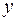– плотность вероятности .