Числовые характеристики системы случайных величин
По аналогии с одномерными СВ для двумерной случайной величины можно записать:
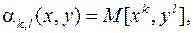
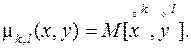 (10.5)
(10.5)
Если говорим о моменте 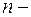 го порядка двумерной СВ, это значит суммируем индексы:
го порядка двумерной СВ, это значит суммируем индексы: 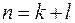 . Для однозначного задания момента двумерной СВ необходимо указать любые два числа из трех:
. Для однозначного задания момента двумерной СВ необходимо указать любые два числа из трех: 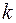 ,
, 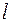 и
и  .
.
Рассмотрим подробнее:
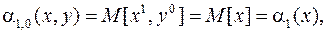


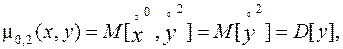
 (10.6)
(10.6)
Как видим для двумерной СВ можно указать три центральных момента второго порядка, особый интерес вызывает смешанный момент.
Ковариацией(или корреляционным моментом) случайных величин  и
и 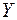 называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий:
называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий:
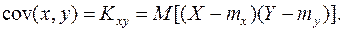 (10.7)
(10.7)
Для дискретной СВ:
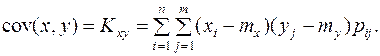 (10.8)
(10.8)
Для непрерывной СВ:
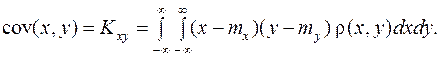 (10.9)
(10.9)
Теорема: Корреляционный момент двух независимых случайных величин  и
и 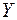 равен нулю.
равен нулю.
Доказательство: (Докажем эту теорему для непрерывных СВ). Пусть  и
и 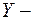 независимые случайные величины, тогда согласно (10.4)
независимые случайные величины, тогда согласно (10.4) 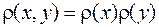 . Подставим это в выражение (10.9)
. Подставим это в выражение (10.9)
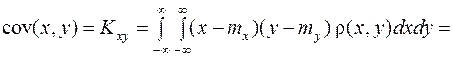
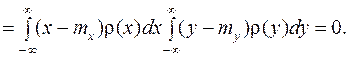 (10.10)
(10.10)
Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки 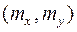 . Если рассеяние (степень разброса) мало, то и ковариация мала.
. Если рассеяние (степень разброса) мало, то и ковариация мала.
Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е.
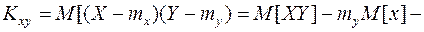
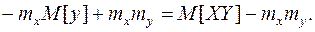 (10.11)
(10.11)
Коэффициентом корреляции двух случайных величин называется отношение ковариации к произведению средних квадратических отклонений этих величин:
 (10.12)
(10.12)
Коэффициент корреляции является безразмерной величиной и не зависит от степени разброса, т.к. функция нормирована на меру разброса 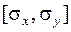 .
.
Пример 1.Имеются линейно зависимые случайные величины, т.е.
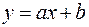 .
.
Необходимо вычислить коэффициент корреляции.
Решение. Пусть для заданной СВ 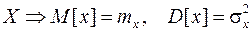 . Тогда, учитывая свойства получим:
. Тогда, учитывая свойства получим:
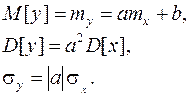
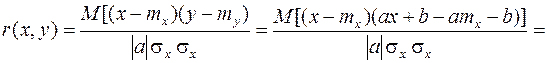
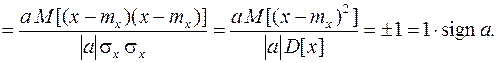
Дата добавления: 2015-06-10; просмотров: 818;
