Показательный (экспоненциальный) закон распределения

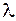Непрерывная случайная величина имеет показательный (экспоненциальный) закон распределения с параметром , если ее плотность вероятности имеет вид:

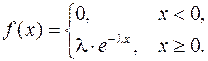(12.1)

Здесь 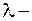постоянная положительная величина. Т.о. показательное распределение определяется одним положительным параметром 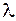. Найдем интегральную функцию показательного распределения:

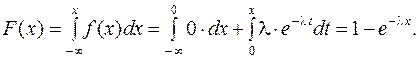(12.2)

Итак,

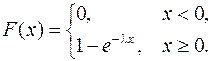(12.3)

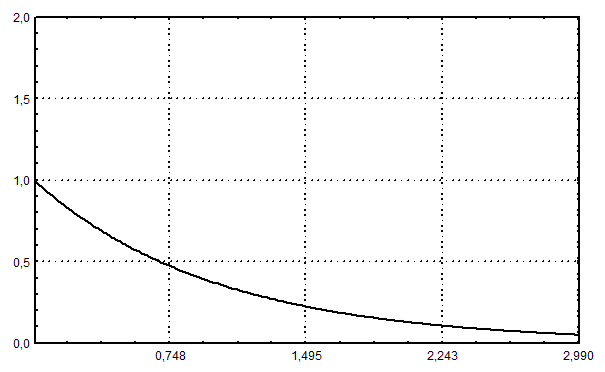
Рис. 12.1. Дифференциальная функция показательного распределения ( )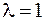

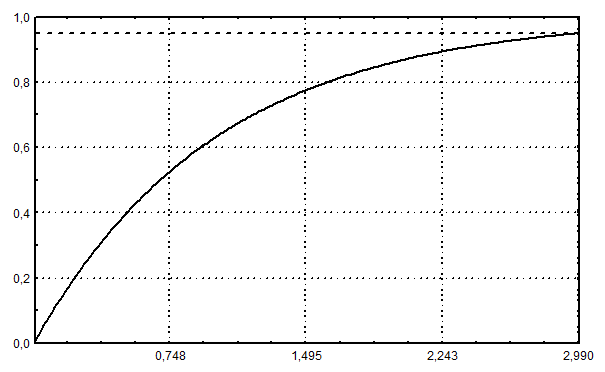
Рис. 12.2. Интегральная функция показательного распределения ( )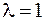

Числовые характеристики показательного распределения

Вычислим математическое ожидание и дисперсию показательного распределения:

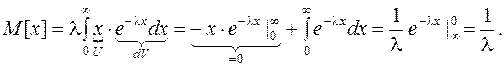(12.4)

Для вычисления дисперсии воспользуемся одним из ее свойств:

(12.5)

Т.к. 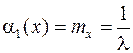, то остается вычислить :

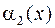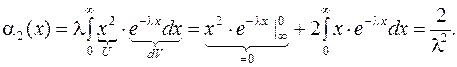(12.6)

Подставив (12.6) в (12.5), окончательно получим:

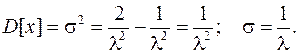(12.7)

Для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению.

Пример 1.Написать дифференциальную и интегральную функции показательного распределения, если параметр .

Решение. а) Плотность распределения имеет вид:

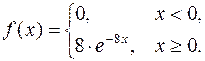
б) Соответствующая интегральная функция равна:

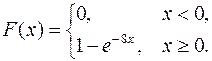
Пример 2.Найти вероятность попадания в заданный интервал 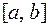для СВ , распределенной по экспоненциальному закону

Решение. Найдем решение, вспомнив, что: 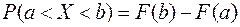. Теперь с учетом (12.3) получим:

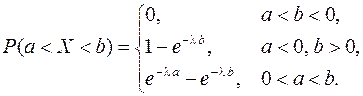
Функция надежности

Будем называть элементом некоторое устройство, независимо от того "простое" оно или "сложное". Пусть элемент начинает работать в момент времени 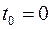, а по истечении времени длительностью 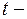происходит отказ. Обозначим через 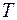непрерывную СВ – длительность времени безотказной работы элемента. Если элемент проработает безотказно (до наступления отказа) время, меньшее чем 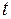, то, следовательно, за время длительностью 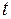наступит отказ. Таким образом, вероятность отказа за время длительностью 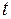определяется интегральной функцией:

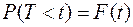. (12.8)

Тогда вероятность безотказной работы за то же время длительностью 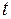равна вероятности противоположного события, т.е.

. (12.9)

Функцией надежности 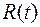называют функцию, определяющую вероятность безотказной работы элемента за время длительностью .

Часто длительность времени безотказной работы элемента имеет показательное распределение, интегральная функция которого равна:

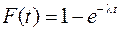. (12.10)

Тогда, в случае показательного распределения времени безотказной работы элемента и с учетом (12.9) функция надежности будет равна:

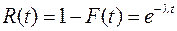. (12.11)

Пример 3.Время безотказной работы элемента распределено по показательному закону 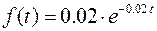при 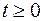( 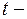время в часах). Найти вероятность того, что элемент проработает безотказно 100 часов.

Решение. В нашем примере 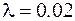, тогда воспользуемся (12.11):

.

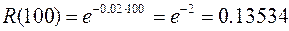Показательный закон надежности весьма прост и удобен для решения практических задач. Этот закон обладает следующим важным свойством:

Вероятность безотказной работы элемента на интервале времени длительностью 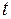не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени 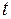(при заданной интенсивности отказов).

Докажем это свойство, введя следующие обозначения:

безотказная работа элемента на интервале длительностью ;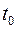

безотказная работа элемента на интервале 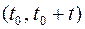длительностью ;

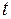Тогда событие 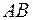состоит в том, что элемент безотказно работает на интервале длительностью 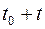. Найдем вероятности этих событий по формуле (12.11), полагая, что время безотказной работы элемента подчинено показательному закону:

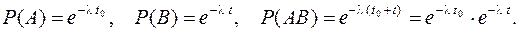(12.12)

Найдем условную вероятность того, что элемент будет работать безотказно на интервале времени 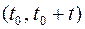при условии, что он уже проработал безотказно на предшествующем интервале времени:

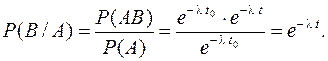(12.13)

Мы видим, что полученная формула не зависит от 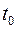, а только от 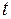. Сравнивая (12.12) и (12.13) можно сделать вывод, что условная вероятность безотказной работы элемента на интервале длительностью 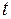, вычисленная в предположении, что элемент проработал безотказно на предшествующем интервале, равна безусловной вероятности.

Итак, в случае показательного закона надежности, безотказная работа элемента "в прошлом" не сказывается на величине вероятности его безотказной работы "в ближайшем будущем".

Элементы комбинаторики

Пространство элементарных событий. Случайные события.

Вероятность

Современное понятие вероятности

Классическая вероятностная схема

Геометрические вероятности

Закон сложения вероятностей

Теорема умножения вероятностей

Формула полной вероятности

Теорема гипотез. Формула Байеса.

Повторение испытаний. Схема Бернулли.

Локальная теорема Муавра-Лапласа

Интегральная теорема Муавра-Лапласа

Теорема Пуассона (Закон редких событий)

Случайные величины

Функции распределения

Непрерывная случайная величина и плотность распределения

Основные свойства плотности распределения

Числовые характеристики одномерной случайной величины

Свойства математического ожидания

Моменты случайной величины

Свойства дисперсии

Асимметрии и эксцесс

Многомерные случайные величины

Свойства двумерной функции распределения

Плотность вероятности двумерной случайной величины

Задача Бюффона

Условная плотность распределения

Числовые характеристики системы случайных величин

Свойства коэффициента корреляции

Нормальный (гауссов) закон распределения

Вероятность попадания на интервал

Свойства нормальной функции распределения

Распределение ("хи–квадрат")

Показательный (экспоненциальный) закон распределения

Числовые характеристики показательного распределения

Функция надежности