Пример 1. Задано распределение вероятностей дискретной двумерной случайной величины: Y X 0.17 0.13 0.25 0.10

Задано распределение вероятностей дискретной двумерной случайной величины:

Y	X

	0.17	0.13	0.25
	0.10	0.30	0.05

Требуется: a) найти законы распределения составляющих и ;
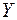b) составить функцию распределения.

Решение а) Сложив вероятности по столбцам, найдем закон распределения составляющей :

X				>12
P	0.27	0.43	0.3
F		0.27	0.7

Сложив вероятности "по строкам", аналогично найдем закон распределения составляющей :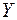

Y			>5
P	0.55	0.45
F		0.55

b) Составим функцию распределения:

Y	X
			>12

		0.17	0.30	0.55
>5		0.27	0.7

Пример 2 (Задача Бюффона)

Иглу длиной 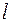бросают на плоскость, на которой на расстоянии 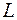друг от друга проведены параллельные линии. Определите вероятность пересечения иглой одной из линий, если .

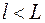Решение. Введем систему случайных величин 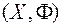, где 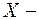расстояние от середины игла до ближайшей линии, а 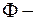острый угол между иглой и линией (см. рис.). Очевидно, что распределено равномерно в интервале 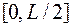, а 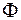распределен равномерно в интервале 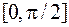. Учитывая, что СВ и 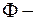независимые, получим 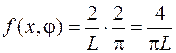при .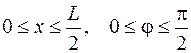

Пересечение иглой одной из линий происходит при заданном угле 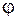, если 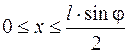. Отсюда получим

<2324 25 26 27 28 29 >

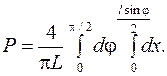
Дата добавления: 2015-06-10; просмотров: 1232;