Свойства нормальной функции распределения

1. 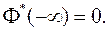2.

3. 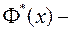функция неубывающая.

4. Из-за симметричности стандартного нормального распределения относительно начала координат следует (см.рис.11.2):

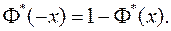
На практике очень часто встречается задача вычисления вероятности попадания СВ на участок симметричный относительно центра рассеивания 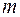. Рассмотрим такой участок длиной 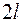. Вычислим эту вероятность:

Рис.11.2. Стандартное распределение

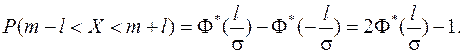(11.17)

Часто расстояние 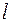выражают в единицах 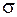. На рис. 11.3. для стандартного нормального распределения показаны вероятности (односторонние) отклониться на .

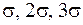Рис.11.3. Свойства нормального закона

Пример.Полагая, что рост студентов – нормально распределенная случайная величина с параметрами и . Необходимо найти:

а) выражение плотности вероятности и функции распределения СВ ;

б) доли костюмов 4-го роста (176 – 182 см) и 3-го роста(170 – 176 см), которые нужно предусмотреть в общем объеме производства;

в) квантиль 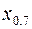и 10%-ную точку СВ ;

г) сформулировать "правило трех сигм" для СВ ;

Решение. а) По формулам (11.1), (11.12) и (11.15) запишем

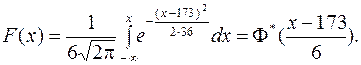
б) Доля костюмов 4-го роста (176 – 182 см) в общем объеме производства определим по формуле (11.16):

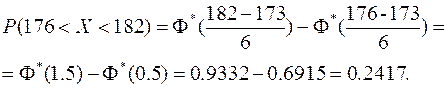
Долю костюмов 3-го роста (170 – 176 см) можно определить аналогичным образом, но, если учесть, что данный интервал симметричен относительно , то по формуле (11.17) оценим:

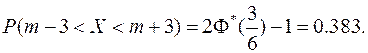
в) Квантиль 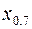СВ найдем из уравнения (11.15):

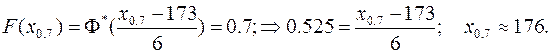
Это значит, что 70% студентов имеют рост до 176 см. 10%-ная точка СВ - это квантиль 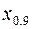, который вычислив аналогично получим .

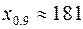г) "Правило трех сигм" для нормального распределения:

.

Тогда с вероятностью равной 0.9974 рост студентов находится в интервале:

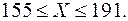
Распределение 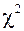("хи–квадрат")

Так называется распределение вероятностей СВ вида:

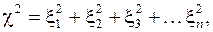(11.18)

где 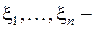независимые случайные величины, имеющие одно и то же нормальное распределение с параметрами 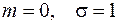. Число называется числом степеней свободы распределения 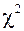. Соответствующая плотность (см. рис.11.4.) описывается формулой:

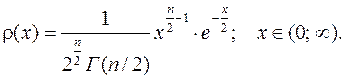(11.19)

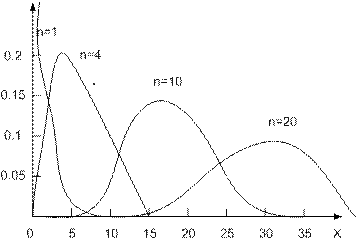
Рис. 11.4. Распределение "хи-квадрат"

Распределение 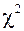представляет собой частный случай так называемого гамма – распределения.