Нормальный (гауссов) закон распределения
Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей. Это наиболее часто встречающийся на практике закон распределения СВ. Главная особенность, выделяющая закон Гаусса, состоит в том, что он является предельным законом, к которому приближаются другие законы при весьма часто встречающихся типичных условиях.
Доказано, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма не жестких ограничениях) приближенно подчиняется нормальному закону. И это свойство выполняется тем точнее, чем большее количество СВ суммируется.
По нормальному закону распределены ошибки измерений, белый шум в электронике и т.п.
Непрерывная случайная величина  имеет нормальный закон распределения(закон Гаусса) с параметрами
имеет нормальный закон распределения(закон Гаусса) с параметрами 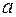 и
и 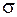 , если ее плотность вероятности определена на всей числовой оси
, если ее плотность вероятности определена на всей числовой оси 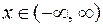 и имеет вид:
и имеет вид:
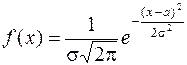 . (11.1)
. (11.1)
Кривую нормального закона распределения называют нормальной  или гауссовой кривой (см. рис. 11.1.). Гауссова кривая имеет симметричный холмообразный вид с максимумом в точке
или гауссовой кривой (см. рис. 11.1.). Гауссова кривая имеет симметричный холмообразный вид с максимумом в точке 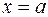 , причем сам максимум равен
, причем сам максимум равен 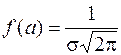 . Выясним смысл параметров
. Выясним смысл параметров 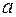 и
и 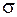 , входящих в (11.1).
, входящих в (11.1).
Рис.11.1. Нормальное распределение
Для этого вычислим сначала математическое ожидание:
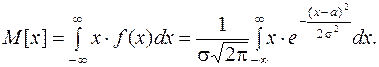 (11.2)
(11.2)
Произведем замену переменных, определив 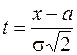 , тогда
, тогда 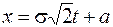 , а
, а 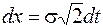 . Подставив в (11.2) получим:
. Подставив в (11.2) получим:
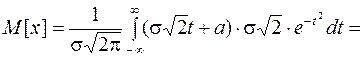
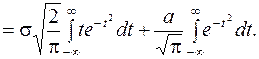 (11.3)
(11.3)
В выражении (11.3) первый интеграл равен нулю, как интеграл от нечетной функции в симметричных относительно начала координат пределах; второй интеграл – это интеграл Пуассона – Эйлера, который равен 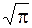 . Тогда окончательно получим:
. Тогда окончательно получим:
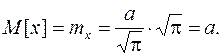 (11.4)
(11.4)
Итак, параметр 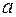 в плотности вероятности нормального распределения равен математическому ожиданию СВ
в плотности вероятности нормального распределения равен математическому ожиданию СВ  .
.
Вычислим теперь дисперсию СВ  :
:
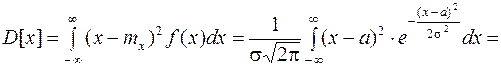
Произведя ту же замену переменных, что и при вычислении математического ожидания, получим:
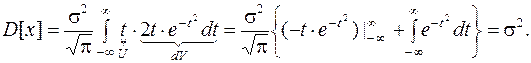 (11.5)
(11.5)
Поясним немного полученный результат. Действительно, первое слагаемое в (11.5) равно нулю, т.к. 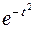 стремится к нулю при
стремится к нулю при 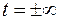 быстрее, чем возрастает любая степень
быстрее, чем возрастает любая степень 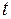 . А второе слагаемое это интеграл Пуассона – Эйлера.
. А второе слагаемое это интеграл Пуассона – Эйлера.
Следовательно, параметр 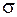 в формуле (11.1) есть не что иное, как среднее квадратическое отклонение СВ
в формуле (11.1) есть не что иное, как среднее квадратическое отклонение СВ  .
.
Выведем общую формулу для центрального момента любого порядка СВ  ,распределенной по нормальному закону. По определению:
,распределенной по нормальному закону. По определению:
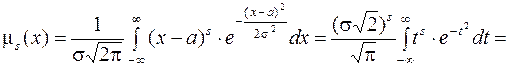
Здесь, как и в предыдущих интегралах применили подстановку, а полученный интеграл будем брать по частям:
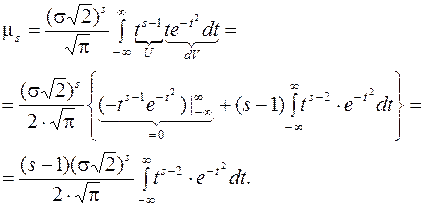 (11.6)
(11.6)
Здесь, при взятии интеграла по частям первое слагаемое равно нулю, т.к. 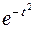 стремится к нулю быстрее, чем возрастает любая степень
стремится к нулю быстрее, чем возрастает любая степень 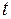 . Теперь запишем центральный момент
. Теперь запишем центральный момент 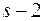 порядка:
порядка:
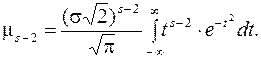 (11.7)
(11.7)
Сравнивая правые части выражений (11.6) и (11.7) получим:
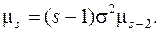 (11.8)
(11.8)
Рекуррентное соотношение (11.8) справедливо для центральных моментов любого порядка. Вспомним, что 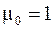 , а
, а 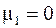 . Тогда все центральные моменты нечетных порядков для нормального распределения равны нулю.
. Тогда все центральные моменты нечетных порядков для нормального распределения равны нулю.
Нормальное распределение симметрично, т.к.:
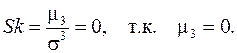 (11.9)
(11.9)
Коэффициент эксцесса нормального распределения, согласно (11.8) равен:
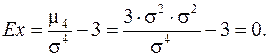 (11.10)
(11.10)
Нормальный закон распределения СВ с параметрами 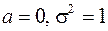 , т.е.
, т.е. 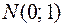 , называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.
, называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.
Вероятность попадания на интервал
Рассмотрим вероятность попадания на интервал 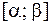 СВ
СВ  , подчиненной нормальному закону распределения с параметрами
, подчиненной нормальному закону распределения с параметрами 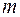 и
и 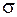 . Для вычисления этой вероятности воспользуемся общей формулой:
. Для вычисления этой вероятности воспользуемся общей формулой:
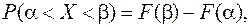 (11.11)
(11.11)
где 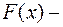 интегральная функция распределения СВ
интегральная функция распределения СВ  . Найдем
. Найдем 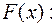
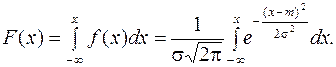 (11.12)
(11.12)
Сделаем замену переменных в (11.12) 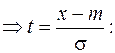
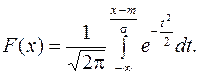 (11.13)
(11.13)
Отметим, что этим преобразованием (заменой переменных) нормальное распределение с произвольными 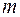 и
и 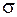 приводится к стандартному нормальному закону с параметрами
приводится к стандартному нормальному закону с параметрами 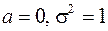 .
.
Интеграл (11.13) не выражается через элементарные функции, но его обычно выражают через специальную функцию, выражающую определенный интеграл от 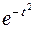 или
или 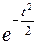 (так называемый интеграл вероятности, для которого составлены статистические таблицы).
(так называемый интеграл вероятности, для которого составлены статистические таблицы).
Вообще существует множество разновидностей таких функций, например:
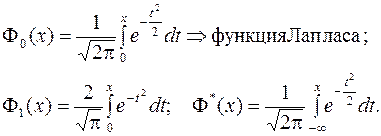 (11.14)
(11.14)
Выберем в качестве такой функции так называемую нормальную функцию распределения 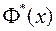 . Выразим функцию распределения (11.13) через
. Выразим функцию распределения (11.13) через 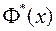 :
:
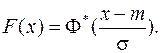 (11.15)
(11.15)
Подставим теперь (11.15) в (11.11):
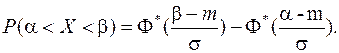 (11.16)
(11.16)
Дата добавления: 2015-06-10; просмотров: 2225;
