Свойства коэффициента корреляции

1. Коэффициент корреляции принимает значения на отрезке :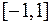

(10.13)

2. Если случайные величины независимы, то их коэффициент корреляции равен нулю. Это свойство верно, т.к. в этом случае .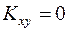

3. Равенство нулю коэффициента корреляции – необходимое, но не достаточное условие независимости случайных величин. Из независимости случайных величин вытекает их некоррелированность. Обратное не всегда верно. Убедимся в этом на примере.

Пример 2.Имеются две СВ: 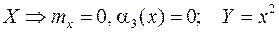. Докажите, что эти величины некоррелированные.

Решение. Вычислим ковариацию:

На практике для 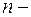мерного случайного вектора достаточно сложно найти закон распределения (интегральную функцию, плотность распределения и т.п.). Поэтому обычно указывают 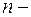математических ожиданий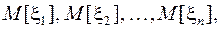 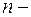дисперси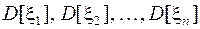й и 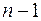корреляционных моментов 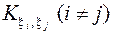, характеризующих парные корреляции всех величин, составляющих вектор . Все корреляционные моменты, дополненные дисперсиями 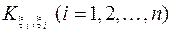, располагают в виде матрицы:

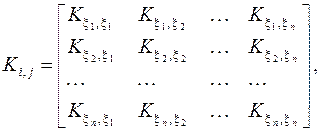(10.14)

которую называют корреляционной матрицей системы случайных величин.

Замечание. Корреляционная матрица симметрична относительно главной диагонали (см. формулы (10.8) и (10.9)).

Пример 2.Двумерная СВ 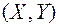задана дифференциальной функцией:

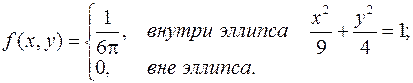
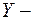Докажите, что и зависимые и не коррелируемые СВ.

Решение. Зная двумерную плотность распределения, вычислим одномерные плотности:

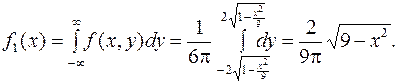
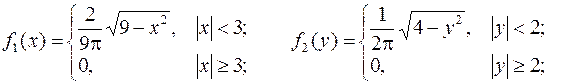
Т.к. 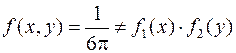, то и 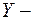зависимые величины. Найдем корреляционный момент: 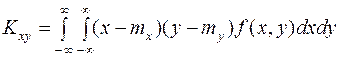. Т.к. функция симметричная относительн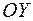о , то 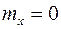, аналогично 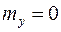. Учитывая эти результаты, получим:

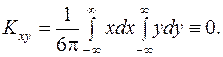
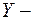Действительно, каждый интеграл от нечетной функции в симметричных пределах равен нулю. Таким образом СВ и зависимые и не коррелируемые.