Асимметрии и эксцесс

Третий центральный момент 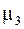служит для характеристики асимметрии (скошенности) распределения.Т.к. третий центральный момент имеет размерность куба случайной величины, то чтобы получить безразмерную характеристику, третий центральный момент делят на куб среднего квадратического отклонения СВ :

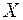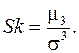(8.23)

Величина 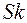называется коэффициентом асимметрии случайной величины.

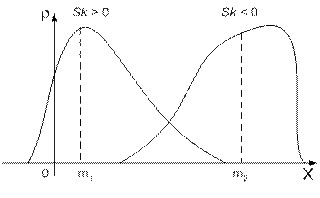
Рис. 8.1. Характеристика асимметрии распределений

На рис.8.1 показаны два распределения, имеющих положительную (распределение 1) и отрицательную (распределение 2) асимметрию. Естественно, что для симметричного распределения .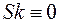

Четвертый центральный момент 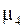служит для характеристики крутости (островершинности) распределения.

Эксцессом случайной величины называется число

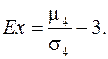(8.24)

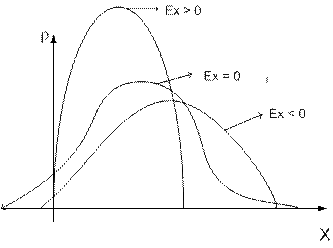
Рис.8.2. Характеристика островершинности распределений

Число 3 в выражении (8.24) вычитается из отношения 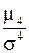потому, что для наиболее часто встречающегося нормального распределения это отношение равно 3. Т.о. распределения более островершинные, чем нормальное имеют положительный эксцесс, распределения с меньшей крутостью, чем нормальное – отрицательный эксцесс, для нормального распределения эксцесс равен нулю (см. рис. 8.2).