Свойства математического ожидания

1. Математическое ожидание постоянной величины равно самой постоянной:

(8.2)

2. Постоянный множитель можно выносить за знак математического ожидания:

(8.3)

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е.

(8.4)

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий (покажем это свойство для двух СВ).

(8.5)

5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю. Пусть математическое ожидание СВ Х равно а, тогда:

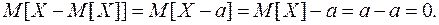(8.6)

Математическое ожидание – одна из характеристик положения СВ. С этой точки зрения математическое ожидание СВ – есть некоторое число, являющееся как бы ее "представителем" и заменяющее при грубых (ориентировочных) расчетах.