Непрерывная случайная величина и плотность распределения

Случайная величина X называется непрерывной, если ее пространством элементарных событий является вся числовая ось (либо отрезок (отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю.

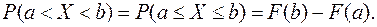(7.1)

Пусть имеется непрерывная СВ 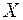с функцией распределения 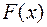, которую мы предполагаем непрерывной и дифференцируемой. Вычислим вероятность попадания этой СВ на участок от 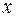до 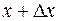, т.е. приращение функции распределения на этом участке:

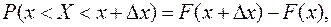(7.2)

Найдем отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать 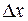к 0. В пределе получим производную от функции распределения, т.е.:

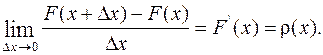(7.3)

Функция 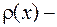производная функции распределения – характеризует плотность, с которой распределяются значения СВ в данной точке.

Эта функция называется плотностью распределения (иначе – "плотностью вероятности") непрерывной СВ X.

Плотность распределения является одной из форм закона распределения. Эта форма не является универсальной, т. к. 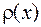существует только для непрерывных СВ. Рассмотрим непрерывную СВ X с плотностью распределения 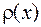и элементарный участок 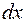, примыкающий к точке .

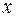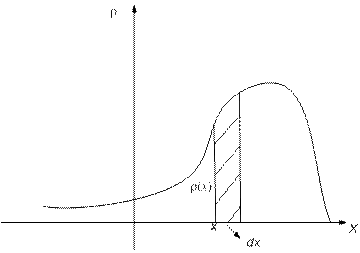
Рис. 7.1. Вероятность попадания на элементарный интервал

Вероятность попадания СВ X на этот элементарный участок(с точность до бесконечно малых высшего порядка) равна 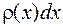. Геометрически – это площадь элементарного прямоугольника, опирающегося на отрезок 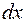(см. рис. 7.1.).

Выразим вероятность попадания СВ X на отрезок от 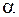до 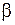через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем участке, т.е. интегралу:

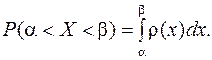(7.4)

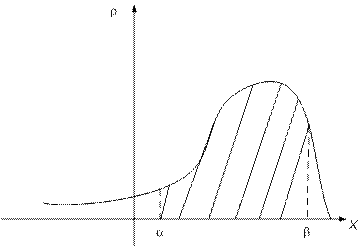
Рис. 7.2. Вероятность попадания на интервал

Т.о. геометрически вероятность попадания величины 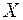на участок 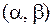равна площади фигуры, ограниченной кривой распределения и опирающейся на этот участок (рис.7.2.).

Формула (7.3) выражает плотность распределения через функцию распределения. Поставим обратную задачу – выразим функцию распределения через плотность. По определению

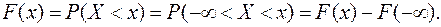(7.5)

Из (7.5) с учетом (7.4) получим:

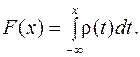(7.6)

Геометрически 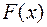есть не что иное, площадь фигуры, ограниченной плотностью распределения (сверху) и осью абсцисс (снизу) и лежащей левее точки 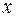(см. рис. 7.3.).

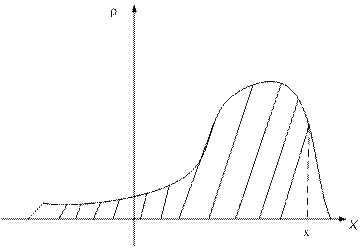
Рис.7.3. Вычисление функции распределения через плотность