Моменты случайной величины

Понятие момента широко применяется в механике для описания распределения масс (статистические моменты, момент инерции и т.п.).

Начальный момент 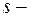го порядка случайной величины 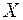обозначается символом 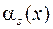и определяется выражением:

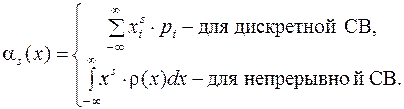(8.7)

Нетрудно убедиться, что введенная выше характеристика математическое ожидание представляет собой не что иное, как первый начальный момент. Используя символ математического ожидания, выражение (8.7) можно представить в следующем виде:

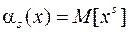. (8.8)

Пусть имеется СВ 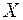с математическим ожиданием 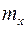. Введем новое понятие.

Центрированной случайной величиной, соответствующей величине 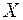, называется отклонение СВ 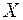от ее математического ожидания:

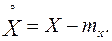(8.9)

Нетрудно показать, что математическое ожидание центрированной СВ равна 0:

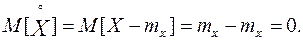(8.10)

Моменты центрированной СВ называются центральными моментами.

Центральным моментом 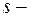го порядка случайной величины 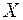называется математическое ожидание 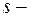й степени соответствующей центрированной СВ:

(8.11)

Очевидно, что для любой СВ центральный момент первого порядка равен нулю.

Второй центральный момент СВ, ввиду его крайней важности среди других характеристик, называется дисперсией и обозначается :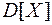

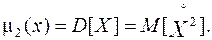(8.12)

Дисперсией 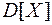случайной величины 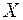называется математическое ожидание квадрата ее отклонения от математического ожидания:

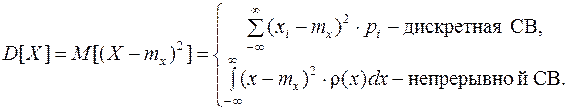(8.13)

Дисперсия СВ характеризует рассеяние (вариацию, разброс) этой величины относительно ее математического ожидания. Дисперсия 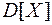имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину .

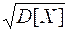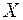Средним квадратическим отклонением (стандартным отклонением или стандартом) случайной величины называется арифметическое значение корня квадратного из ее дисперсии:

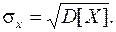(8.14)