Многомерные случайные величины
Очень часто результат испытания характеризуется не одной случайной величины, а некоторой системой случайных величин 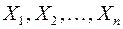 , которую называют также многомерной (
, которую называют также многомерной ( 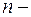 мерной) случайной величиной или случайным вектором
мерной) случайной величиной или случайным вектором 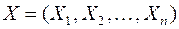 .
.
Случайные величины 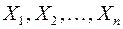 , входящие в систему, могут быть как дискретными, так и непрерывными.
, входящие в систему, могут быть как дискретными, так и непрерывными.
Приведем примеры многомерных случайных величин:
· физическое состояние человека можно охарактеризовать системой случайных величин: 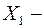 рост,
рост, 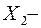 вес,
вес, 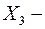 возраст, и т.п.
возраст, и т.п.
· успеваемость студента можно описать многомерной случайной величиной 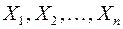 , где
, где  оценка по
оценка по 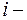 му предмету.
му предмету.
Геометрически двумерную и трехмерную случайные величины можно интерпретировать случайной точкой (вектором) на плоскости  или в трехмерном пространстве
или в трехмерном пространстве  . Как отмечалось ранее, наиболее полным описанием СВ является закон ее распределения. Дальнейшее рассмотрение многомерных СВ проведем на примере двумерных случайных величин.
. Как отмечалось ранее, наиболее полным описанием СВ является закон ее распределения. Дальнейшее рассмотрение многомерных СВ проведем на примере двумерных случайных величин.
Определим, как и для одномерной СВ, интегральную функцию распределения двумерной СВ:
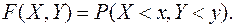 (9.1)
(9.1)
 Геометрически функция распределения
Геометрически функция распределения 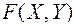 означает вероятность попадания случайной точки
означает вероятность попадания случайной точки 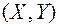 в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки M(X,Y) (рис. 9.1). Правая и верхняя границы области в квадрант не включаются – это значит, что функция распределения непрерывна слева по каждому из аргументов.
в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки M(X,Y) (рис. 9.1). Правая и верхняя границы области в квадрант не включаются – это значит, что функция распределения непрерывна слева по каждому из аргументов.
В случае дискретной двумерной случайной величины ее функция распределения определяется по формуле:
Рис. 9.1.
 (9.2)
(9.2)
Здесь (9.2) суммирование вероятностей производится по всем значениям 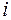 , для которых
, для которых  и по всем
и по всем 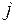 , для которых
, для которых 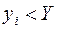 .
.
Дата добавления: 2015-06-10; просмотров: 1244;
