Теорема сложения вероятностей.
(4) 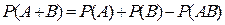 для совместных событий.
для совместных событий.
(5) 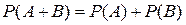 для несовместных событий.
для несовместных событий.
Доказательство для несовместных событий.
Пусть имеется n возможных классических исходов.
Пусть m из них благоприятствуют событию А
и пусть k других (других, т.к. события несовместные и у них нет благоприятствующих исходов) исходов благоприятствуют событию В.
Тогда событию А+В благоприятствуют m+k исходов, т.е.
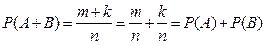 , что и требовалось доказать.
, что и требовалось доказать.
Следствие № 1: Теорема о сложении (формула 5) распространяется на любое конечное число несовместных событий (может быть 3, 4, 5…слагаемых).
Следствие № 2: Если события А1, А2, А3, …образуют полную группу, то сумма их вероятностей равна 1.
(6) 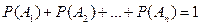 полная группа
полная группа
Доказательство:
Если события образуют полную группу, то их сумма является достоверным событием, вероятность которого равна 1, т.е.
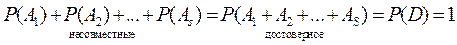
Следствие № 3: Для противоположных событий справедливо равенство:
(7) 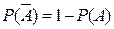
Пример:
В пруду плавает 100 рыб. Из них 20 щук и 10 лещей. Случайным образом ловят одну рыбу.
А) Какова вероятность того что это щука или лещ.
Б) Какова вероятность что это рыба другого сорта
Решение:
А – щука; В – лещ.
А) 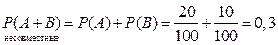
Б) 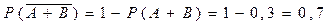
Дата добавления: 2015-05-26; просмотров: 854;
