Обчислення площ фігур за допомогою визначеного інтеграла.
Площа криволінійної трапеції, обмеженої кривою y = f (x), віссю ОХ і двома прямими х = а і b, де 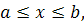 f(x)
f(x) 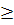 0, обчислюється за формулою:
0, обчислюється за формулою:
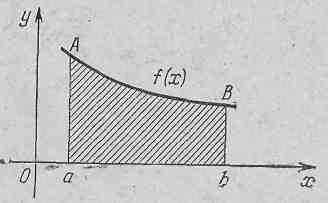
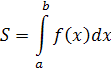
Якщо криволінійна трапеція обмежена кривою y = f (x) 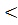 0,віссю ОХ і прямими х = а і х = b лежить під віссю ОХ, то площу знаходять за формулою:
0,віссю ОХ і прямими х = а і х = b лежить під віссю ОХ, то площу знаходять за формулою:
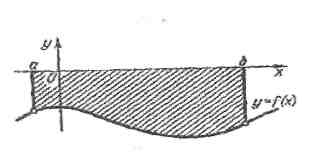
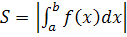
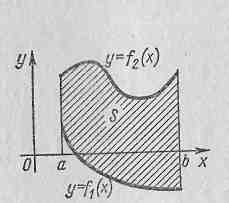
Якщо фігура обмежена двома кривими, що перетинаються, з яких 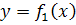 і
і 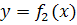 і прямими х = а і x = b, де
і прямими х = а і x = b, де 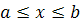 і
і
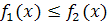 , тоді її площу знаходять за формулою
, тоді її площу знаходять за формулою
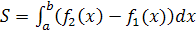
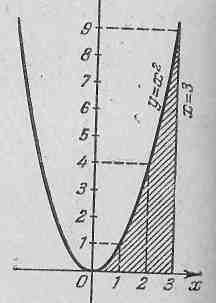
Приклад 1. Обчислити площу фігури, обмеженої лініями у = х2,у = 0 і х = 3.
Розв’язання.
Побудуємо цю фігуру.
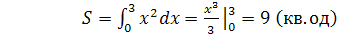
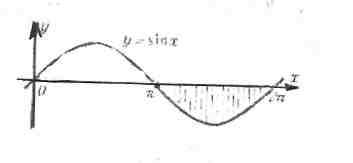
Приклад 2. Обчислити площу фігури, обмеженої лініями у = sinx,у = 0 і
х = 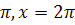 .
.
Розв’язання.
Побудуємо цю фігуру.
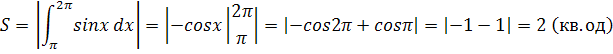
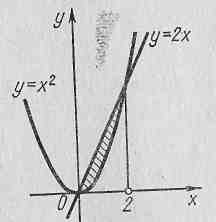
Приклад 3. Обчислити площу фігури, обмеженої лініями у = х2,у = 2х
Розв’язання.
Побудуємо цю фігуру. Для знаходження точок перетину ліній розв’яжемо систему рівнянь:
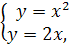
звідки знаходимо 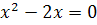
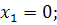
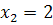
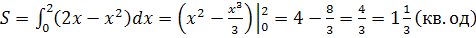
Дата добавления: 2015-06-27; просмотров: 20464;
