Amp; 6.6. Методи інтегрування частинами та заміною змінних у визначеному інтегралі.
При обчисленні визначеного інтеграла методом заміни змінної визначений інтеграл 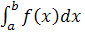 перетворюється за допомогою підстановки φ(x) = t у визначений інтеграл відносно нової змінної t. При цьому старі межі інтегрування a і
перетворюється за допомогою підстановки φ(x) = t у визначений інтеграл відносно нової змінної t. При цьому старі межі інтегрування a і 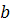 замінюють відповідно новими межами інтегрування, які знаходять із підстановки.
замінюють відповідно новими межами інтегрування, які знаходять із підстановки.
Формула інтегрування частинами для визначеного інтеграла має вигляд:
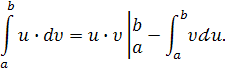
Приклад 1. Обчисліть визначений інтеграл: 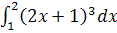 .
.
Розв'язання.
Введемо підстановку: 2х + 1= t. Диференціюючи, маємо: 2dx = dt, звідки 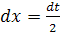 . Знаходимо нові межі інтегрування: tн= 2 ∙ 1 + 1 = 3, tв = 2 ∙ 2 + 1 = 5. Маємо:
. Знаходимо нові межі інтегрування: tн= 2 ∙ 1 + 1 = 3, tв = 2 ∙ 2 + 1 = 5. Маємо:
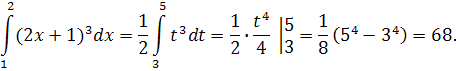
Приклад 2. Обчисліть визначений інтеграл: 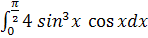 .
.
Розв'язання .
Введемо підстановку: 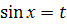 . Диференціюючи, маємо
. Диференціюючи, маємо 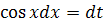 . Знаходимо нові межі інтегрування tн =
. Знаходимо нові межі інтегрування tн = 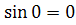 , tв =
, tв = 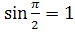 . Маємо:
. Маємо:
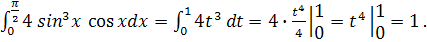
Приклад 3. Обчисліть визначений інтеграл:
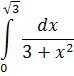
Розв’язання.
Перетворимо підінтегральний вираз:
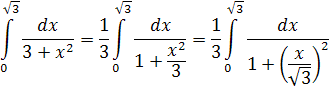
Введемо підстановку: 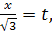 тоді
тоді 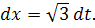 Знаходимо нові межі:
Знаходимо нові межі: 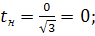
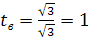
Підставимо в інтеграл:
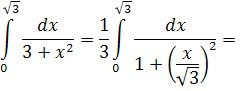
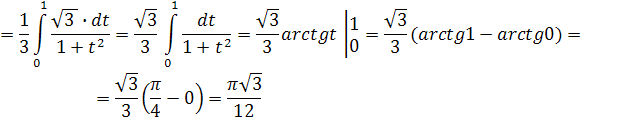
Приклад 4. Обчисліть визначений інтеграл:
s New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>.</m:t></m:r></m:e></m:nary></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 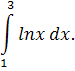
Розв’язання.
Застосовуємо формулу інтегрування частинами, вважаючи 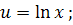
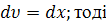
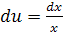 ;
; 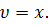 Отже
Отже 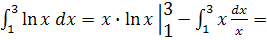
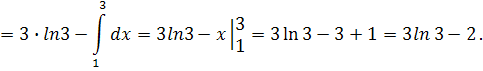
Дата добавления: 2015-06-27; просмотров: 4006;
