Апертурный угол и числовая апертура оптического волокна

Измерение апертуры и потерь в соединениях строительных длин оптических кабелей

Апертурный угол и числовая апертура оптического волокна

Апертурным углом многомодового оптического волокна называется угол между оптической осью волокна и одной из образующих светового конуса, опадающего в торец волокна, при котором выполняется условие полного внутреннего отражения лучей на границе раздела «сердцевина-оболочка». Лучи, находящиеся внутри указанного конуса, представляют совокупность мод, направляемых волокном. Синус апертурного угла есть числовая апертура волокна. При определении числовой апертуры в качестве внешней среды берется воздух, который имеет коэффициент преломления n₀=1. В этих условиях величина апертурного угла апертуры зависят от значений коэффициентов преломления сердцевины волокна n₁ и оболочки волокна n₂.

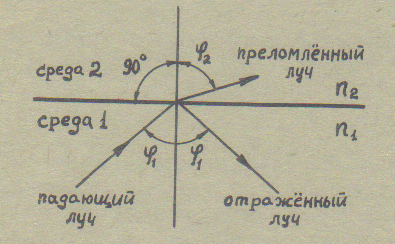
Рис.1. Лучевая картина на границе раздела оптических сред

На рис.1 показана модель распространения лучей на границе разделения двух оптических сред с коэффициентами преломления n₁ и n₂, причем n₁ > n₂. Падающий луч, который имеет угол падения φ₁, в общем случае испытывает отражение под углом φ₁ и преломление под углом φ₂. При этом

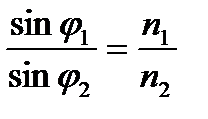(1)

Положив φ₂ = 90°, имеем 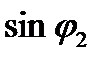= 1, т.е. преломленный луч направлен вдоль границы раздела. Кроме того, его энергия имеет нулевое значение. Обозначив в данном случае φ₁ = φ*, из (1) получаем:

sin φ* = 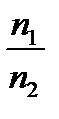(2)

При угле φ* луч в среду 2 не поступает и весь отражается в среду 1, т.е. происходит полное внутреннее отражение оптической энергии. Угол полного внутреннего отражения, определенный по (2), представляет собой критическую величину угла падения. Все лучи, которые имеют φ* < φ₁ < 90°, также испытывают полное внутреннее отражение на границе раздела.

В соответствии с изложенным, апертурный угол ступенчатого волокна связан с углом φ*, имеющим место на границе раздела сердцевины и оболочки.

Лучевая модель условий ввода оптической энергии в волокно представлена на рис.2, где из всей совокупности лучей точечного источника, расположенного на оси световода, выделены траектории трех лучей.

Луч 1 имеет угол падения φ < φ*, поэтому при достижении границы раздела часть его энергии выходит в оболочку и излучается из волокна. Таким же образом происходят и дальнейшие отражения этого луча. В результате переносимая им энергия на коротком расстоянии от начала волокна (в пределах 3 м) полностью высвечивается и, следовательно, не участвует в процессе распространения сигналов по волокну.

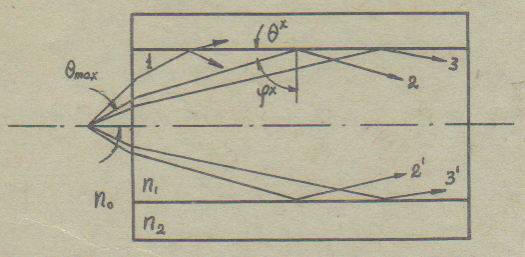
Рис.2. Лучевая картина ввода в ступенчатое волокно

Луч 2 (и симметричный ему луч 2’) падает на границу раздела с углом, равным φ* и, следовательно, испытывает полное внутреннее отражение. Таким образом, энергия, переносимая этим лучом, полностью удерживается в сердцевине и сигнал передается по волокну. В аналогичных условиях находятся все лучи, имеющие угол падения больше φ*, в том числе, луч 3 (и симметричный ему луч 3’). Отсюда следует, что все лучи, находящиеся внутри кругового конуса в пределах Q_max, распространяется по световоду, т.е. Q_max является его апертурным углом.

С использованием (1), (2) и геометрических соотношений рис.2, имеем:

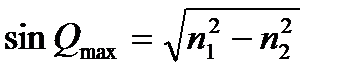(3)

где Q_max определяется в радіанах.

Так как n₁ – n₂ = Δn << n₁, то Q_max << 1 и величина апертурного угла

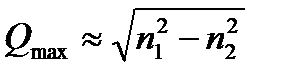(4)

Согласно (3), числовая апертура оптического волокна

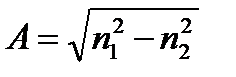(5)

Преобразуя (5), получаем:

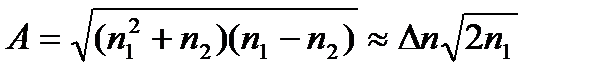(6)

В кварцевых волокнах n₁, n₂ = 1,45 +1,50, поэтому можно записать:

А ≈ 1,7Δn (7)

где Δn – абсолютная величина разности коэффициентов преломления сердцевины и оболочки волокна.

Таким образом, если известна величина апертуры, то можно легко рассчитать значение Δn и обратно.

В градиентных волокнах апертурные свойства несколько сложнее; при смещении точечного источника с оси волокна величина апертурного угла изменяется. Однако в целом оказывается возможность применять определенные выше апертурные характеристики, используя в качестве величины n₁ значение коэффициента преломления на оси волокна.

Как видно из (4) – (7), числовая апертура и апертурный угол волокна тем больше, чем больше величину имеет разность коэффициентов преломления Δn. Для примера, взяв Δn =0,01, с помощью (7) получаем А = 0,17. Волокна, имеющие апертуру не более 0,2, называются низкоапертурными волокнами; волокна, имеющие апертуру более 0,2, называются высокоапертурными волокнами. Поскольку А однозначно связано с Δn, то величина числовой апертуры волокна характеризует ряд его важных передаточных параметров, зависящих от разности коэффициентов преломления.

Чем больше числовая апертура, тем больше уширение импульсов из-за модовой дисперсии:

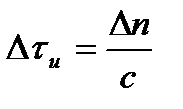, с/км (8)

больше величина обобщенного параметра волокна:

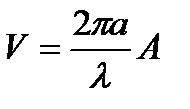(9)

больше количество направляемых волн:

N= (10)

меньше потери на изгибах:

Δа_из= 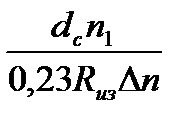, дБ (11)

С ростом апертуры уменьшаются потери энергии на вводе в волокно при использовании источников с широкой диаграммой направленности излучения.

В выражениях (8) – (11) использованы величины: с = 3·10⁵ км/с, а – радиус сердцевины в мкм, d_c и R_из – диаметр сердцевины и радиус изгиба волокна (берутся в одной и той же размерности, например, мм).

Как следует из изложенного, высокоапертурные волокна обеспечивают сравнительно низкие потери на воде и сравнительно мало чувствительны к изгибам. Однако они имеют сравнительно низкую пропускную способность за счет большей модовой дисперсии. Поэтому высокоапертурные волокна применяются для передачи оптических сигналов на короткие расстояния, в пределах помещения или объекта. В оптических кабелях, предназначающихся для применения на сетях связи, используются низкоапертурные волокна.