Рух тіл у в’язкому середовищі

Коли тіло рухається у середовищі з в’язкістю, на нього діє сила опору, яка виникає внаслідок тертя між нерухомими шарами рідини і шарами, які рухаються разом з тілом. Згідно з міркуваннями, наведеними у попередньому параграфі, можна очікувати, що в першому наближенні сила опору буде пропорційна швидкості руху тіла відносно рідини. Експеримент підтверджує цей висновок тільки за умови, що швидкість руху невелика. (Яку швидкість можна вважати невеликою, обговорюється в параграфі 8.14). Отже, будемо вважати, що сила опору 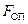пропорційна швидкості, тобто

.

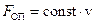Зокрема, якщо у в’язкому середовищі рухається сферичне тіло радіуса 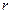, то сила опору дорівнює

.

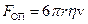Остання формула називається формулою Стокса.

Нижче розглянуто два приклади руху кульки радіуса 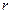у в’язкому середовищі.

8.12.1. Нехай кулька радіуса 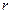розпочала рух з початковою швидкістю 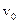. Єдина сила, що діє на кульку під час руху, є сила тертя. Рівняння руху кульки буде

,

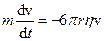де 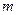- маса кульки, 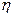- коефіцієнт в’язкості середовища. Після інтегрування отримаємо

,

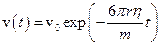тобто швидкість кульки експоненційно спадає з характерним часом загасання

.

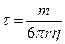Чим більша в’язкість середовища, тим швидше загасає рух тіла. Приблизно так буде поводити себе, наприклад, човен на воді, якого штовхнули з невеликою початковою швидкістю.

8.12.2. Рух кулі у в’язкому середовищі під дією сталої сили.

Нехай у початковий момент часу 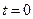до кульки маси 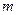, яка знаходилась у спокої, приклали сталу силу 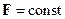, під дією якої вона почне рухатись у напрямку дії сили. Запишемо рівняння руху

.

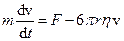Отримане рівняння – лінійне диференціальне рівняння із сталими коефіцієнтами. Розв’язок його відомий:

.

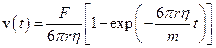Проаналізуємо отриманий результат. Залежність швидкості руху тіла від часу представляє собою плавно зростаючу функцію, яка в границі 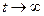асимптотично наближується до значення швидкості 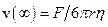. Графік функції 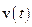наведено на рис.8.19. Там же наведено графік зміни з часом прискорення тіла. Видно, що рух тіла не є рівноприскореним. З початку руху прискорення зменшується від максимального значення 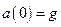до нуля при 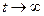. Характерний час встановлення сталої швидкості, 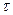, звичайно визначають як час, за який прискорення зменшується в 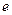разів: .

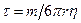Приблизно так буде поводити себе, наприклад, кулька, яка тоне у рідині під дією сталої сили тяжіння, або човен, що рухається за допомогою двигуна.