Кінематичний опис руху рідини. Теорема нерозривності

Гідродинаміка вивчає рух рідин. Явища, розглядувані в гідродинаміці, мають макроскопічний характер, і рідина розглядається як суцільне середовище. Це означає, що будь-який малий елемент об'єму рідини вважається настільки великим, що містить в собі дуже велику кількість молекул. Відповідно до цього, коли в гідродинаміці кажуть про нескінченно малий елемент об'єму, то завжди мають на увазі, що він досить малий у порівнянні з об'ємом тіла, але великий у порівнянні з відстанями між молекулами. У такому ж контексті треба розуміти поняття “частинка рідини” або “точка рідини”, якими користуються для опису руху рідин і газів. Якщо, наприклад, у механіці кажуть про рух певної частинки рідини, то при цьому мова йде не про рух окремої молекули, а про зсув елемента об'єму, що містить велику кількість молекул.

Таким чином, математично описати рух рідини можна двома способами. Так, можна простежити за рухом кожної окремої частинки рідини, тобто визначити положення і швидкість цієї частинки в кожний момент часу. Тим самим будуть відомі і траєкторії всіх частинок рідини. Такий спосіб опису розроблявся Лагранжем. Існує простіший підхід до опису руху рідин. Основна його ідея полягає в тому, щоб спостерігати не за окремими частинками рідини, а за певними точками простору і визначати швидкість (точніше її модуль та напрямок), з якою проходять через кожну точку окремі частинки рідини в різні моменти часу. Такий спосіб називається методом Ейлера. Якщо охопити всі точки простору і фіксувати час t, то при другому способі опису руху рідин утвориться просторова картина розподілу швидкостей в рідині – поле швидкостей.

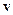Поле швидкостей можна зобразити наступним чином. Проведемо в рідині, яка рухається, лінії таким чином, щоб дотична до них у кожній точці збігалася за напрямком з вектором (рис. 8.6). Ці лінії називаються лініями струму.

Якщо поле швидкостей, а отже, і відповідні йому лінії струму не змінюються з часом, то рух рідини називається стаціонарним або сталим. Якщо ж вони змінюються в часі, то рух називається нестаціонарним. У випадку нестаціонарного руху при другому способі опису швидкість рідини залежить від координат і часу: 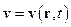і лінії струму не збігаються з траєкторіями частинок рідини. При стаціонарному русі залежності 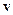від часу немає, і швидкість залежить тільки від координат: 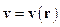. Тільки при стаціонарному русі лінії струму збігаються з траєкторіями частинок.

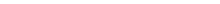Оберемо довільний замкнений контур і проведемо лінії струму через кожну точку його в певний момент часу (рис. 8.7). Ці лінії утворять поверхню, яка називається трубкою струму.

Вектор 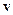швидкості часток рідини спрямований по дотичний до ліній струму, а значить при русі частинки рідини не будуть перетинати бічну поверхню трубки струму.

Трубка струму (яка є уявною) поводить себе подібно то бокової поверхні реальної трубки, в якій тече рідина. На такі трубки струму можна розбити весь простір, в якому відбувається рух рідини.

Розглянемо два поперечні перерізи 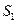і 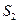, які перпендикулярні до осьової лінії струму АВ (рис.8.8). Поперечний переріз трубок струму зазвичай обирають настільки малим, щоб можна було вважати швидкість однаковою в межах будь-якого її поперечного перерізу і спрямованою вздовж осі трубки струму. Частинки рідини, які в певний момент часу 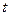знаходились в поперечному перерізі 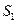, через нескінченно малий проміжок часу 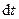пройдуть шлях, рівний 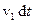, і опиняться в перерізі 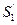. Звідси випливає, що за час 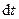через поперечний переріз 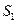проходить об’єм рідини:

.

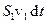В той же час через поперечний переріз 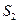пройде об’єм рідини:

.

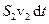Якщо рідина нестиснена, то через обидва перерізи повинні пройти однакові об’єми рідини. Звідси

.

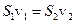Наведені міркування справедливі для будь-яких двох поперечних перерізів трубки струму. Тому, в загальному випадку для трубки струму можна вважати

,

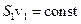тобто добуток швидкості течії нестисненої нев’язкої рідини та поперечного перерізу трубки струму є величина стала для даної трубки струму. Це твердження відомо як теорема нерозривності. З теореми нерозривності випливає, що швидкість рідини в трубці струму буде тим більша, чим вужчий поперечний переріз трубки. Швидкість в трубці обернено пропорційна площі даного поперечного перерізу.