Розподіл тиску в нерухомих рідинах і газах. Закон Паскаля

8.2.1. Розглянемо окремий випадок, коли зовнішні об’ємні сили відсутні, тобто 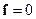. Тоді, з основного рівняння гідростатики випливає, що

.

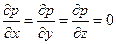Отже, за відсутності об’ємних сил, при рівновазі тиск у всіх точках рідини однаковий. Наведене твердження є законом Паскаля. Зокрема, якщо немає об’ємних (масових) сил, то рідина може перебувати в рівновазі лише тоді, коли зовнішній тиск на її поверхню однаковий в усіх точках цієї поверхні. В супротивному випадку виникає рух рідини. За відсутності об’ємних сил однаковий тиск на поверхню рідини зумовлює появу такого самого тиску в усіх точках рідини. Тобто, за законом Паскаля, в рівноважному стані рідини і гази передають тиск, прикладений до них, рівномірно за усіма напрямками.

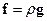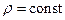8.2.2. Розглянемо окремий випадок, коли рідина перебуває в полі тяжіння, тобто , де (наближення абсолютно нестисненої рідини). Спрямуємо вісь Z вздовж сили тяжіння. Основне рівняння гідростатики в такому випадку набуде вигляду:

.

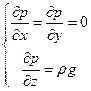Після інтегрування останнього рівняння отримаємо:

,

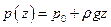де 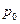– тиск на висоті 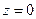, тобто атмосферний тиск, якщо початок координат збігається з вільною поверхнею рідини. З отриманого розв’язку видно, що тиск не залежить від координат x та y, і залишається сталим у площинах 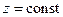. Такі горизонтальні площини називаються площинами рівного тиску. Тиск, зумовлений висотою стовпа рідини, називається гідростатичним тиском. Відзначимо, що величина атмосферного тиску ~ 10⁵ Па, а густина води 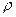=10³ кг/м³. В такому випадку, з отриманого рівняння можна підрахувати, що із збільшенням глибини у воді на кожні 10 м, тиск додатково зростає на величину атмосферного тиску. Так, на глибині 100 м тиск .

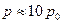8.2.3. Важливим є той факт, що зростання тиску з глибиною не залежить від форми посудини, в якій знаходиться рідина. Ілюстрацією цього є рівність рівнів рідини в посудинах різного розміру, які сполучені між собою (рис.8.2,а). Рівність двох тисків в нижній частині посудини, яка забезпечує рівновагу рідини, можлива лише за умови рівних висот стовпчиків води в цих посудинах.

Змінимо умови експерименту і розташуємо в нижній горизонтальній частині U-подібної посудини рухому перепону, яка не дозволяє змішуватись двом рідинам з різними густинами (рис.8.2, б). Нехай ліва частина заповнена рідиною з більшою густиною, наприклад ртуттю, а права – водою. Очевидно, що рівновага буде при різних висотах стовпчиків рідин. Висота стовпчику ртуті 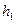буде дорівнювати:

,

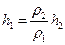де 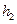– висота стовпчика води, а 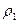і 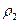– густини ртуті і води, відповідно. Слід відзначити, що висота стовпчика ртуті буде приблизно в 10 разів меншою за висоту стовпчику води, оскільки густина ртуті приблизно на порядок перевищує густину води. Варто пам’ятати, що стовпчик ртуті, висотою 760 мм, врівноважує тиск майже десятикілометрового стовпа атмосфери. Тому атмосферний тиск іноді вимірюють у міліметрах ртутного стовпчика.

8.2.4. Таким чином, сила тиску рідини на дно посудини не залежить від її форми, а залежить тільки від площі дна, різниці рівнів поверхні рідини і дна, а також від густини рідини. Так, ця сила буде однією і тією ж для всіх трьох посудин, зображених на рис.8.3, якщо вони мають однакову площу дна, а рідина налита до однакового рівня. Тоді здається логічним припустити, що при зважуванні зображених на рис.8.3 посудин із рідиною ваги мали б показувати однакову вагу, оскільки показання ваг залежить від сили, із яким дно посудини давить на чашку ваг. Виникає так званий гідростатичний парадокс. Що ж в дійсності покажуть ваги? Ваги покажуть різну вагу посудин рис.8.3. Розглянемо в чому ж полягає помилка у наведеному міркуванні, яке призводить до гідростатичного парадоксу. Він знімається, якщо врахувати те, що ваги вимірюють силу тиску посудини на чашку, яка дорівнює силі, з якою рідина діє на всю посудину, а не тільки на дно. Тобто, слід також враховувати суму сил, що діють з боку рідини на бокові стінки посудини. Зокрема, для першої посудини (див. рис.8.3) така сума спрямована донизу, а для третьої посудини – навпаки догори. Загальна рівнодійна сил для всіх посудин буде дорівнювати вазі рідини.