Принцип еквівалентності

Сили інерції, що діють на тіла в неінерційній системі відліку, пропорційні їхнім масам і за інших рівних умов надають цим тілам однакові відносні прискорення. Іншими словами, всі тіла, вільні від зовнішніх впливів, рухаються в “полі сил інерції”, тобто відносно неінерційної системи відліку, цілком однаково, якщо тільки початкові умови їх руху також однакові. Така ж закономірність спостерігається при рухові відносно інерційних систем відліку тіл, на які діють сили гравітаційного поля. У кожній точці поля ці сили, подібно силам інерції, пропорційні масам тіл і надають усім тілам однакові прискорення вільного падіння, рівні напруженості поля в розглядуваній його точці.

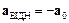Наприклад, в неінерційній системі відліку, пов¢язаній із ліфтом, який рухається рівноприскорено вертикально вгору з переносним прискоренням , всі вільні тіла падають за відсутності поля тяжіння з однаковим відносним прискоренням . Точнісінько так же поводять себе вільні тіла в тому ж ліфті, що рухається рівномірно в однорідному гравітаційному полі напруженістю 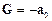. Таким чином, на основі експериментів з вільного падіння тіл усередині щільно зачиненого ліфта неможливо встановити, чи рухається ліфт рівномірно в полі тяжіння напруженістю 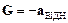(зокрема, ліфт може бути в спокої в цьому полі) чи він рухається зі сталим переносним прискоренням 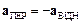за відсутності гравітаційного поля.

Локальний принцип еквівалентності: гравітаційне поле в обмеженій ділянці простору фізично еквівалентне (рівновартне) “полю сил інерції” у відповідним чином вибраній неінерційній системі відліку. Ділянка простору повинна бути настільки малою, щоб поле тяжіння в ній можна було вважати однорідним.

Принцип еквівалентності не слід розуміти як твердження про тотожність сил інерції та сил ньютонівського тяжіння між тілами. Справді, напруженість істинного гравітаційного поля, створюваного тілами, спадає в міру віддалення від цих тіл і на нескінченності обертається в нуль. Поля тяжіння, “рівновартні” силам інерції, не задовольняють цю умову. Наприклад, напруженість гравітаційного поля, “еквівалентного” відцентровим силам інерції в системі відліку, що обертається, необмежено зростає в міру віддаляння від осі обертання. Напруженість поля, “рівновартного” переносним силам інерції в системі відліку, яка рухається поступально, всюди однакова.

Істинне гравітаційне поле, на відміну від “еквівалентного” силам інерції, існує як у неінерційних, так і в інерційних системах відліку. Ніяким вибором неінерційної системи відліку неможливо повністю виключити істинне гравітаційне поле, тобто скомпенсувати його в усьому просторі “полем сил інерції”. Це випливає хоча б із різної поведінки “полів сил інерції” та істинних полів тяжіння на нескінченності. Таке виключення гравітаційного поля можна здійснити лише локально, тобто для малої області простору, в межах якої це поле можна вважати однорідним, і для проміжку часу, протягом якого поле можна вважати сталим. Відповідна цій операції неінерційна система відліку повинна рухатися з переносним прискоренням, рівним прискоренню вільного падіння тіл у розглядуваній області істинного гравітаційного поля. Так, у космічному кораблі, який здійснює вільний політ у гравітаційнному полі, сили тяжіння компенсуються переносними силами інерції і не спричиняють відносного руху тіл на кораблі.