Сили інерції

В інерційних системах відліку єдиною причиною прискореного руху тіла є сили, які діють на нього з боку інших тіл. Сила завжди є результат взаємодії матеріальних тіл. В неінерційних системах відліку тіло може рухатись з прискоренням лише за рахунок зміни стану руху системи відліку. Наприклад, якщо обрати за систему відліку автомобіль, який рухається з прискоренням, то небесні тіла (Сонце, Місяць та інші) в такій системі відліку будуть мати прискорення. Природно, що такі прискорення не є результатом дії на них яких-небудь сил з боку інших тіл. Таким чином, в неінерційних системах відліку існують прискорення, які не пов’язані з силами такого самого характеру, які відомі для інерційних систем відліку.

В неінерційних системах відліку закони Ньютона не виконуються. Зокрема, матеріальна точка може змінювати стан свого руху відносно неінерційної системи відліку S без будь-якого впливу на цю точку з боку інших тіл. Наприклад, кулька, підвішена на нитці до стелі вагона поїзда, який рухається рівномірно та прямолінійно, відхилюється назад при прискоренні поїзда і вперед – при його сповільненні, тобто починає рухатися відносно неінерційної системи відліку, пов¢язаної з вагоном. При цьому ніякі горизонтальні сили на кульку не діють.

Для побудови теорії руху в неінерційних системах відліку фактори, які зумовлюють прискорення, були визнані за сили. Причому, ці сили зв’язані з прискореннями такими самими співвідношеннями, що і “звичайні” сили. При цьому, передбачається, що в неінерційних системах, так само, як і в інерційних, прискорення зумовлені лише силами. Проте, поруч зі “звичайними” силами, з якими ми мали справу раніше, існують також сили особливої природи, які називають силами інерції. Такий підхід дозволяє сформулювати закони Ньютона без змін, якщо поруч з силами взаємодії врахувати сили інерції.

Основний закон динаміки матеріальної точки в неінерційних системах відліку можна одержати, виходячи з другого закону Ньютона і зв¢язку між абсолютним і відносним прискореннями матеріальної точки. Добуток маси 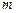матеріальної точки на її відносне прискорення дорівнює:

.

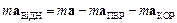Згідно з другим законом Ньютона, застосованим до абсолютного руху матеріальної точки, тобто до її руху відносно інерційної системи відліку К,

,

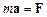де 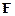– геометрична сума всіх сил, що діють на матеріальну точку. Отже, основне рівняння динаміки відносного руху матеріальної точки має вигляд:

.

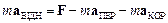Його можна звести до виразу, аналогічного за формою основному закону динаміки абсолютного руху точки:

.

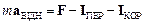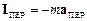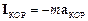Векторні величини і мають розмірність сили і називаються відповідно переносною силою інерції та коріолісовою силою інерції.

В загальному випадку переносна сила інерції дорівнює сумі трьох доданків:

.

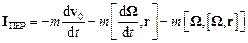Останній доданок правої частини цього виразу

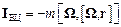
називається відцентровою силою інерції або просто відцентровою силою, через те що цей вектор перпендикулярний до миттєвої осі обертання (до вектора 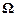) неінерційної системи відліку S і спрямований від цієї осі. Чисельно відцентрова сила дорівнює:

,

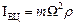де 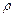– відстань від матеріальної точки маси m до миттєвої осі обертання системи відліку.

Переносна сила інерції збігається з відцентровою, якщо неінерційна система відліку рухається поступально зі сталою швидкістю ( 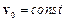) і обертається зі сталою кутовою швидкістю ( ).

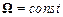Коріолісова сила інерції дорівнює

.

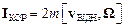Ця сила діє на матеріальну точку тільки тоді, коли неінерційна система відліку обертається, а матеріальна точка рухається відносно неї. Так, наприклад, на частинки води в річках, які течуть у меридіональному напрямку, діють коріолісові сили інерції, що спрямовані перпендикулярно до швидкості течії ріки і спричиняють підмивання одного з берегів (у Північній півкулі - правого за течією берега).

Коріолісова сила інерції не виконує роботи у відносному русі матеріальної точки, оскільки ця сила спрямована перпендикулярно до швидкості відносного руху точки. Отже, коріолісова сила інерції є прикладом гіроскопічних сил.

Сили інерції реальні в тому ж сенсі, в якому реальними є прискорення, що існують в неінерційних системах відліку. Вони також реальні в більш глибокому розумінні: при розгляді сил інерції можна вказати конкретні прояви їх дії. Сили інерції, що діють на матеріальну точку в неінерційній системі відліку і можуть бути виміряні, наприклад, за допомогою пружинного динамометра. Так, в вагоні потягу, який набирає швидкість, пасажир відчуває на собі дію сили, яка спрямована проти руху потягу. Якщо ж пасажир сидить по ходу потягу, то сила інерції притискає його до спинки сидіння. Якщо ж потяг гальмує, то сила інерції в такому випадку буде намагатися віддалятиме тіло людини від спинки.

Проте, на відміну від звичайних сил взаємодії тіл, щодо сил інерції не можна сказати, дію яких конкретно тіл на розглядувану матеріальну точку вони відтворюють. Ця особливість сил інерції пов¢язана з тим, що сама поява векторних величин 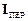і 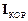в основному рівнянні динаміки відносного руху зумовлена лише неінерційністю системи відліку, який використовується для опису відносного руху точки. Додання до сили 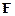, яка характеризує дію на матеріальну точку всіх інших тіл, сил інерці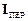ї і 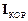дозволяє записати основне рівняння динаміки відносного руху в формі, схожій на запис другого закону Ньютона в інерційній системі відліку.

У неінерційних системах відліку не може бути замкнених систем тіл, оскільки для будь-якого з тіл системи сили інерції завжди є зовнішніми силами. Тому в неінерційних системах відліку не виконуються закони збереження імпульсу, моменту імпульсу та енергії.