Приклад 3. Момент інерції кулі відносно осі, що проходить через її центр.
У цьому випадку доцільно застосувати сферичну систему координат (рис.1.3). Спрямуємо вісь OZ уздовж осі обертання. Елемент об’єма 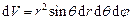 має масу
має масу 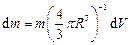 (тут
(тут 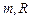 - маса і радіус кулі). Як видно з рис.1.3, елемент
- маса і радіус кулі). Як видно з рис.1.3, елемент 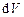 розташований на відстані
розташований на відстані 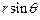 від осі. Аналогічно попереднім прикладам, момент інерції кулі отримаємо інтегруванням
від осі. Аналогічно попереднім прикладам, момент інерції кулі отримаємо інтегруванням
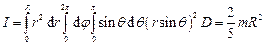
(Примітка: при інтегруванні застосуйте формулу 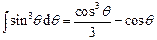 ).
).
Моменти інерції однорідних тіл найпростішої форми відносно деяких осей наведено у таблиці 4.1.
Таблиця 4.1
| Тіло | Положення осі | Момент інерції |
| Порожнистий тонкостінний циліндр радіусом R і масою m | Вісь циліндра | mR2 |
| Суцільний циліндр (диск) радіусом R і масою m | Вісь циліндра | mR2/2 |
| Куля радіусом R і масою m | Вісь проходить через центр кулі | (2/5) mR2 |
| Тонкостінна сфера радіусом R і масою m | Вісь проходить через центр сфери | (2/3) mR2 |
| Прямий тонкий стержень довжиною l і масою m | Вісь перпендикулярна до стержня і проходить через його середину | ml2/12 |
Момент інерції тіла, як і його маса, характеризують інертність тіла. Але, на відміну від маси, момент інерції не є характеристикою тіла як такого. Значення моменту інерції залежить не тільки від маси, форми і розмірів тіла, але і від вибору положення осі відносно тіла. Одне і те ж тіло відносно різних осей має різні значення моменту інерції. Іншими словами, не можна казати: “Момент інерції Землі дорівнює приблизно 9.7·1037 кг м2“, у той час як вислів “маса Землі приблизно дорівнює 6·1024 кг” цілком правильний. (До речі, сучасні дані свідчать, що момент інерції Землі відносно власної осі обертання не відповідає значенню, яке можна отримати за вищенаведеною формулою для однорідної кулі, 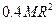 . Відомо, що цей момент інерції помітно менший, ніж очікується за розрахунками, а саме дорівнює близько
. Відомо, що цей момент інерції помітно менший, ніж очікується за розрахунками, а саме дорівнює близько 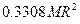 . Ця обставина вказує на те, що густина Землі суттєво збільшується з глибиною.)
. Ця обставина вказує на те, що густина Землі суттєво збільшується з глибиною.)
Згідно з теоремою Штейнера (теоремою про перенесення осей інерції), момент інерції тіла 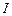 відносно довільної осі дорівнює сумі моменту інерції цього тіла
відносно довільної осі дорівнює сумі моменту інерції цього тіла 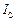 відносно осі, яка проходить через центр інерції тіла паралельно (!) розглядуваній осі, і добутку маси тіла m на квадрат відстані
відносно осі, яка проходить через центр інерції тіла паралельно (!) розглядуваній осі, і добутку маси тіла m на квадрат відстані 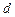 між осями:
між осями:
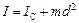 .
.
Наприклад, повернемось до рис.4.3 і розрахуємо момент інерції стержня відносно осі, що проходить через його центр мас перпендикулярно до стержня. Очевидно, центр мас знаходиться посередині стержня, тобто 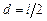 . Застосуємо теорему Штейнера, і отримаємо:
. Застосуємо теорему Штейнера, і отримаємо:
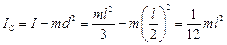 .
.
Дата добавления: 2015-04-07; просмотров: 4425;
